单选题 (共 8 题 ),每题只有一个选项正确
实数 2 的倒数是 ( )
$\text{A.}$ -2
$\text{B.}$ 2
$\text{C.}$ $-\frac{1}{2}$
$\text{D.}$ $\frac{1}{2}$
“致中和,天地位焉,万物育焉”,对称之美随处可见.下列选项分别是扬州大学、扬州中国大运河博物馆、扬州五亭桥、扬州志愿服务的标识.其中的轴对称图形是
$\text{A.}$  $\text{B.}$
$\text{B.}$  $\text{C.}$
$\text{C.}$  $\text{D.}$
$\text{D.}$ 
下列运算中正确的是 ( )
$\text{A.}$ $(a-b)^2=a^2-b^2$
$\text{B.}$ $5 a-2 a=3 a$
$\text{C.}$ $\left(a^3\right)^2=a^5$
$\text{D.}$ $3 a^2 \cdot 2 a^3=6 a^6$
第8个全国近视防控宣传教育月的主题是“有效减少近视发生,共同守护光明未来”.某校积极响应,开展视力检查.某班45名同学视力检查数据如下表:
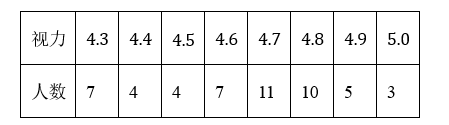
这45名同学视力检查数据的众数是
$\text{A.}$ 4.6
$\text{B.}$ 4.7
$\text{C.}$ 4.8
$\text{D.}$ 4.9
在平面直角坐标系中, 点 $P(1,2)$ 关于原点的对称点 $P^{\prime}$ 的坐标是
$\text{A.}$ $(1,2)$
$\text{B.}$ $(-1,2)$
$\text{C.}$ $(1,-2)$
$\text{D.}$ $(-1,-2)$
如图是某几何体的表面展开后得到的平面图形,则该几何体是
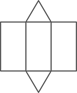
$\text{A.}$ 三棱锥
$\text{B.}$ 圆锥
$\text{C.}$ 三棱柱
$\text{D.}$ 长方体
在平面直角坐标系中,函数 $y=\frac{4}{x+2}$ 的图像与坐标轴的交点个数是()
$\text{A.}$ 0
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ 4
1202 年数学家斐波那契在《计算之书》中记载了一列数: $1,1,2,3,5, \cdots \cdots$ ,这一列数满足:从第三个数开始,每一个数都等于它的前两个数之和。则在这一列数的前 2024 个数中,奇数的个数为()
$\text{A.}$ 676
$\text{B.}$ 674
$\text{C.}$ 1348
$\text{D.}$ 1350
填空题 (共 10 题 ),请把答案直接填写在答题纸上
近年来扬州经济稳步发展: 2024年4月26日, 扬州市统计局、国家统计局扬州调查队联合发布一季度全市实现地区生产总值约 18700000 万元, 把 18700000 这个数用科学记数法表示为
某学习小组做抛掷一枚瓶盖的实验,整理的实验数据如表:
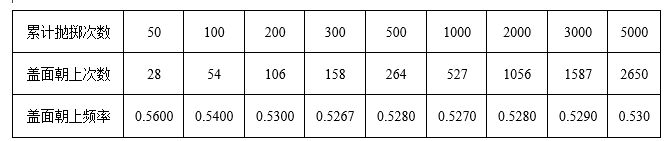
随着实验次数的增大, "盖面朝上" 的概率接近于 $\qquad$ (精确到 0.01 ).
若二次根式 $\sqrt{x-2}$ 有意义, 则 $x$ 的取值范围是
若用半径为 10 cm 的半圆形纸片围成一个圆锥的侧面, 则这个圆锥底面圆的半径为
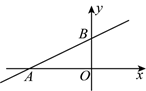
如图, 已知一次函数 $y=k x+b(k \neq 0)$ 的图象分别与 $x 、 y$ 轴交于 $A 、 B$ 两点, 若 $O A=2, O B=1$, 则关于 $x$ 的方程 $k x+b=0$ 的解为
《九章算术》是中国古代的数学专著, 是《算经十书》中最重要的一部, 书中第八章内容 "方程"里记载了一个有趣的追及问题, 可理解为: 速度快的人每分钟走 100 米, 速度慢的人每分钟走 60 米, 现在速度慢的人先走 100 米, 速度快的人去追他. 问速度快的人追上他需要 $\qquad$ 分钟.

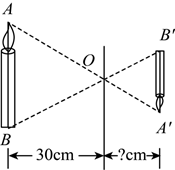
物理课上学过小孔成像的原理, 它是一种利用光的直线传播特性实现图像投影的方法. 如图, 燃烧的蜡烛(坚直放置) $A B$ 经小孔 $O$ 在屏幕(坚直放置)上成像 $A^{\prime} B^{\prime}$ 。设 $A B=36 \mathrm{~cm}, A^{\prime} B^{\prime}=24 \mathrm{~cm}$ 。小孔 $O$ 到 $A B$ 的距离为 30 cm , 则小孔 $O$ 到 $A^{\prime} B^{\prime}$ 的距离为 $\qquad$ cm.
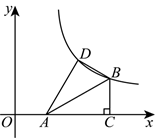
如图, 在平面直角坐标系中, 点 $A$ 的坐标为 $(1,0)$, 点 $B$ 在反比例函数 $y=\frac{k}{x}(x>0)$ 的图像上, $B C \perp x$轴于点 $C, \angle B A C=30^{\circ}$, 将 $\triangle A B C$ 沿 $A B$ 翻折, 若点 $C$ 的对应点 $D$ 落在该反比例函数的图像上, 则 $k$ 的值为 . $\qquad$
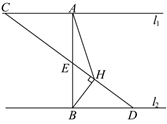
如图, 已知两条平行线 $l_1 、 l_2$, 点 $A$ 是 $l_1$ 上的定点, $A B \perp l_2$ 于点 $B$, 点 $C 、 D$ 分别是 $l_1 、 l_2$ 上的动点,且满足 $A C=B D$, 连接 $C D$ 交线段 $A B$ 于点 $E, B H \perp C D$ 于点 $H$, 则当 $\angle B A H$ 最大时, $\sin \angle B A H$ 的值为
解答题 (共 10 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
(1) 计算: $|\pi-3|+2 \sin 30^{\circ}-(\sqrt{5}-2)^0$;
(2) 化简: $\frac{x-2}{x+1} \div(x-2)$.
解不等式组 $\left\{\begin{array}{c}2 x-6 \leq 0 \\ x < \frac{4 x-1}{2}\end{array}\right.$, 并求出它的所有整数解的和.
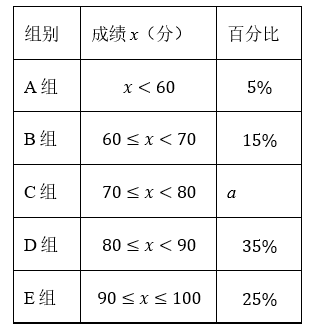
2024 年 5 月 28 日, 神舟十八号航天员叶光富、李聪、李广苏密切协同, 完成出舱活动, 活动时长达 8.5 小时,刷新了中国航天员单次出舱活动时间纪录,进一步激发了青少年热爱科学的热情. 某校为了普及 "航空航天" 知识, 从该校 1200 名学生中随机抽取了 200 名学生参加 "航空航天" 知识测试, 将成绩整理绘制成如下不完整的统计图表:
成绩统计表
成绩条形统计图
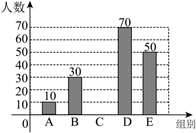
根据所给信息, 解答下列问题:
(1) 本次调查的成绩统计表中 $a=$ $\qquad$ \%, 并补全条形统计图;
(2) 这 200 名学生成绩的中位数会落在 $\qquad$ 组 (填 $A 、 B 、 C 、 D$ 或E);
(3) 试估计该校 1200 名学生中成绩在 90 分以上 (包括 90 分) 的人数.
2024年"五一"假期,扬州各旅游景区持续火热。小明和小亮准备到东关街、瘦西湖、运河三湾风景区、个园、何园(分别记作 $A 、 B 、 C 、 D 、 E$ )参加公益讲解活动.
(1) 若小明在这 5 个景区中随机选择 1 个景区, 则选中东关街的概率是 $\qquad$ ;
(2) 小明和小亮在 $C 、 D 、 E$ 三个景区中,各自随机选择 1 个景区,请用画树状图或列表的方法,求小明和小亮选到相同景区的概率.
为了提高垃圾处理效率, 某垃圾处理厂购进 $A 、 B$ 两种机器, $A$ 型机器比 $B$ 型机器每天多处理 40 吨垃圾, $A$ 型机器处理 500 吨垃圾所用天数与 $B$ 型机器处理 300 吨垃圾所用天数相等. $B$ 型机器每天处理多少吨垃圾?
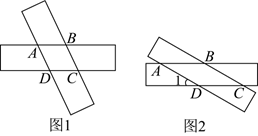
如图 1, 将两个宽度相等的矩形纸条叠放在一起, 得到四边形 $A B C D$.
(1) 试判断四边形 $A B C D$ 的形状, 并说明理由;
(2) 已知矩形纸条宽度为 2 cm , 将矩形纸条旋转至如图 2 位置时, 四边形 $A B C D$ 的面积为 $8 \mathrm{~cm}^2$, 求此时直线 $A D 、 C D$ 所夹锐角 $\angle 1$ 的度数.
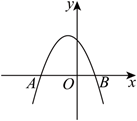
如图, 已知二次函数 $y=-x^2+b x+c$ 的图像与 $x$ 轴交于 $A(-2,0), B(1,0)$ 两点.
(1) 求 $b 、 c$ 的值;
(2) 若点 $P$ 在该二次函数的图像上, 且 $\triangle P A B$ 的面积为 6 , 求点 $P$ 的坐标.
如图, 已知 $\angle P A Q$ 及 $A P$ 边上一点 $C$.
(1) 用无刻度直尺和圆规在射线 $A Q$ 上求作点 $O$, 使得 $\angle C O Q=2 \angle C A Q$; (保留作图痕迹, 不写作法)
(2) 在 (1) 的条件下, 以点 $O$ 为圆心, 以 $O A$ 为半径的圆交射线 $A Q$ 于点 $B$, 用无刻度直尺和圆规在射线 $C P$
上求作点 $M$, 使点 $M$ 到点 $C$ 的距离与点 $M$ 到射线 $A Q$ 的距离相等; (保留作图痕迹, 不写作法)
(3) 在 (1)、(2) 的条件下, 若 $\sin A=\frac{3}{5}, C M=12$, 求 $B M$ 的长.
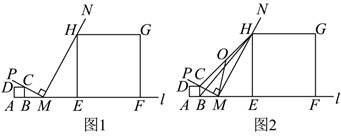
如图, 点 $A 、 B 、 M 、 E 、 F$ 依次在直线 $l$ 上, 点 $A 、 B$ 固定不动, 且 $A B=2$, 分别以 $A B 、 E F$ 为边在直线 $l$ 同侧作正方形 $A B C D$ 、正方形 $E F G H, \angle P M N=90^{\circ}$, 直角边 $M P$ 恒过点 $C$, 直角边 $M N$ 恒过点 $H$.
(1) 如图1, 若 $B E=10, E F=12$, 求点 $M$ 与点 $B$ 之间的距离;
(2) 如图1, 若 $B E=10$, 当点 $M$ 在点 $B 、 E$ 之间运动时, 求 $H E$ 的最大值;
(3) 如图2, 若 $B F=22$, 当点 $E$ 在点 $B 、 F$ 之间运动时, 点 $M$ 随之运动, 连接 $C H$, 点 $O$ 是 $C H$ 的中点, 连接 $H B 、 M O$, 则 $2 O M+H B$ 的最小值为
在综合实践活动中, "特殊到一般" 是一种常用方法, 我们可以先研究特殊情况, 猜想结论, 然后再研究一般情况, 证明结论.
如图, 已知 $\triangle A B C, C A=C B, \odot O$ 是 $\triangle A B C$ 的外接圆, 点 $D$ 在 $\odot O$ 上 $(A D>B D)$, 连接 $A D 、 B D 、 C D$.
【特殊化感知】
(1) 如图 1, 若 $\angle A C B=60^{\circ}$, 点 $D$ 在 $A O$ 延长线上, 则 $A D-B D$ 与 $C D$ 的数量关系为 $\qquad$ ;
【一般化探究】
(2) 如图 2, 若 $\angle A C B=60^{\circ}$, 点 $C 、 D$ 在 $A B$ 同侧, 判断 $A D-B D$ 与 $C D$ 的数量关系并说明理由;
【拓展性延伸】
(3) 若 $\angle A C B=\alpha$, 直接写出 $A D 、 B D 、 C D$ 满足的数量关系. (用含 $\alpha$ 的式子表示)