在综合实践活动中, "特殊到一般" 是一种常用方法, 我们可以先研究特殊情况, 猜想结论, 然后再研究一般情况, 证明结论.

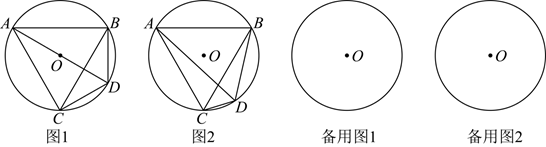
如图, 已知 $\triangle A B C, C A=C B, \odot O$ 是 $\triangle A B C$ 的外接圆, 点 $D$ 在 $\odot O$ 上 $(A D>B D)$, 连接 $A D 、 B D 、 C D$.
【特殊化感知】
(1) 如图 1, 若 $\angle A C B=60^{\circ}$, 点 $D$ 在 $A O$ 延长线上, 则 $A D-B D$ 与 $C D$ 的数量关系为 $\qquad$ ；

【一般化探究】
(2) 如图 2, 若 $\angle A C B=60^{\circ}$, 点 $C 、 D$ 在 $A B$ 同侧, 判断 $A D-B D$ 与 $C D$ 的数量关系并说明理由;

【拓展性延伸】
(3) 若 $\angle A C B=\alpha$, 直接写出 $A D 、 B D 、 C D$ 满足的数量关系. (用含 $\alpha$ 的式子表示)