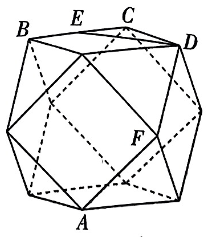
很多立体图形都体现了数学的对称美,其中半正多面体是由两种或两种以上的正多边形围成的多面体,半正多面体因其最早由阿基米德研究发现,故也被称作阿基米德体. 如图, 这是一个棱数为 24 , 棱长为 $\sqrt{2}$ 的半正多面体, 它的所有顶点都在同一个正方体的表面上,可以看成是由一个正方体截去八个相同的四面体所得,则下列各选项正确的是
A
该半正多面体的体积为 $\frac{20}{3}$
B
$A, C, D, F$ 四点共面
C
该半正多面体外接球的表面积为 $12 \pi$
D
若 $E$ 为线段 $B C$ 上的动点, 则直线 $D E$ 与直线 $A F$ 所成角的余弦值的取值范围为$\left[\frac{1}{2}, \frac{\sqrt{2}}{2}\right]$
E
F