单选题 (共 6 题 ),每题只有一个选项正确
已知命题 $p: \forall x \in R ,|x+1|>1$; 命题 $q: \exists x>0, x^3=x$. 则
$\text{A.}$ $p$ 和 $q$ 都是真命题
$\text{B.}$ $\neg p$ 和 $q$ 都是真命题
$\text{C.}$ $p$ 和 $\neg q$ 都是真命题
$\text{D.}$ $\neg p$ 和 $\neg q$ 都是真命题
已知向量 $a =(1,1), b =(1,-1)$. 若 $( a +\lambda b ) \perp( a +$ $\mu b$ ), 则
$\text{A.}$ $\lambda+\mu=1$
$\text{B.}$ $\lambda+\mu=-1$
$\text{C.}$ $\lambda \mu=1$
$\text{D.}$ $\lambda \mu=-1$
已知向量 $a , b , c$ 满足 $| a |=| b |=1,| c |=\sqrt{2}$, 且 $a + b +$ $c = 0$, 则 $\cos \langle a - c , b - c \rangle=$
$\text{A.}$ $-\frac{4}{5}$
$\text{B.}$ $-\frac{2}{5}$
$\text{C.}$ $\frac{2}{5}$
$\text{D.}$ $\frac{4}{5}$
若 $2^a+\log _2 a=4^b+2 \log _4 b$, 则
$\text{A.}$ $a>2 b$
$\text{B.}$ $a < 2 b$
$\text{C.}$ $a>b^2$
$\text{D.}$ $a < b^2$
已知数列 $\left\{\frac{1}{4 n^2+4 n-3}\right\}$ 的前 $n$ 项和为 $T_n$, 若对任意的 $n \in N ^*$, 不等式 $6 T_n < 3 a^2-a$ 恒成立, 则实数 $a$ 的取值范围是
$\text{A.}$ $\left(-\infty,-\frac{2}{3}\right] \cup[1,+\infty)$
$\text{B.}$ $(-\infty,-1] \cup\left[\frac{2}{3},+\infty\right)$
$\text{C.}$ $\left[-\frac{2}{3}, 1\right]$
$\text{D.}$ $\left(-\infty,-\frac{2}{3}\right) \cup(1,+\infty)$
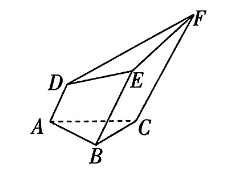
一个五面体 $A B C-D E F$. 已知 $A D / / B E / / C F$, 且两两之间距离为 $1, A D=1, B E=2, C F=3$, 则该五面体的体积为
$\text{A.}$ $\frac{\sqrt{3}}{6}$
$\text{B.}$ $\frac{3 \sqrt{3}}{4}+\frac{1}{2}$
$\text{C.}$ $\frac{\sqrt{3}}{2}$
$\text{D.}$ $\frac{3 \sqrt{3}}{4}-\frac{1}{2}$
多选题 (共 1 题 ),每题有多个选项正确
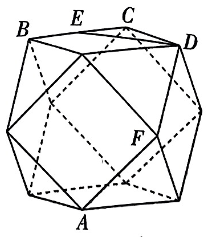
很多立体图形都体现了数学的对称美,其中半正多面体是由两种或两种以上的正多边形围成的多面体,半正多面体因其最早由阿基米德研究发现,故也被称作阿基米德体. 如图, 这是一个棱数为 24 , 棱长为 $\sqrt{2}$ 的半正多面体, 它的所有顶点都在同一个正方体的表面上,可以看成是由一个正方体截去八个相同的四面体所得,则下列各选项正确的是
$\text{A.}$ 该半正多面体的体积为 $\frac{20}{3}$
$\text{B.}$ $A, C, D, F$ 四点共面
$\text{C.}$ 该半正多面体外接球的表面积为 $12 \pi$
$\text{D.}$ 若 $E$ 为线段 $B C$ 上的动点, 则直线 $D E$ 与直线 $A F$ 所成角的余弦值的取值范围为$\left[\frac{1}{2}, \frac{\sqrt{2}}{2}\right]$