如图, 曲线 $C$ 称为"双纽线", 其对称中心在坐标原点 $O$, 且 $C$ 上的点满足到点 $F_1(-a$, $0)$ 和 $F_2(a, 0)$ 的距离之积为定值 $a^2$, 则
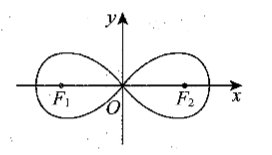
A
若 $a=1$, 点 $(\sqrt{2}, 0)$ 在曲线 $C$ 上
B
若 $a=1$, 曲线 $C$ 的方程为 $\left(x^2+y^2\right)^2=2 x^2-y^2$
C
若 $a=2$, 曲线 $C$ 上点的纵坐标的最大值为 1
D
若点 $\left(x_0, y_0\right)$ 在 $C$ 上, 则 $\left|y_0\right| \leqslant\left|x_0\right|$
E
F