单选题 (共 8 题 ),每题只有一个选项正确
设全集 $U=\{1,2,3,5,7\}$, 集合 $A=\{1, a \cdots 2,7\}, \complement_U A=\{3,5\}$, 则 $a$ 的值是
$\text{A.}$ 4
$\text{B.}$ 5
$\text{C.}$ 7
$\text{D.}$ 9
对于非零向量 $a , b , a / / b$ 是 $a -3 b =0$ 的
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分也不必要条件
已知 $b>\frac{1}{a}>1$, 则
$\text{A.}$ $a b < 1$
$\text{B.}$ $2^a+2^b>4$
$\text{C.}$ $\log _a 2>\log _b 2$
$\text{D.}$ $a^b>b^a$
已知等差数列 $\left\{a_n\right\}$ 的公差为 $d, a_1=1$, 若 $a_1, a_3, a_7$ 成等比数列, 则 $d$ 等于
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ 2
$\text{C.}$ 0 或 $\frac{1}{2}$
$\text{D.}$ 0 或 2
函数 $f(x)$ 在区间 $\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$ 上的大致图象如图所示, 则 $f(x)$ 的解析式可能是
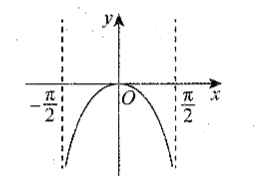
$\text{A.}$ $f(x)=\tan (|\sin x|)$
$\text{B.}$ $f(x)=\tan (\cos x)$
$\text{C.}$ $f(x)=\ln (|\sin x|)$
$\text{D.}$ $f(x)=\ln (\cos x)$
已知 $\alpha, \beta, \gamma$ 是三个不同的平面, $l, m, n$ 是三条不同的直线,下列结论正确的是
$\text{A.}$ 若 $m / / n, n \subset \alpha$, 则 $m / / \alpha$
$\text{B.}$ 若 $\alpha / / \beta, m \subset \alpha, n \subset \beta$, 则 $m / / n$
$\text{C.}$ 若 $\alpha \perp \gamma, \beta \perp \gamma$, 则 $\alpha / / \beta$
$\text{D.}$ $\alpha \cap \beta=l, \beta \cap \gamma=m, \alpha \cap \gamma=n$, 则三条交线 $l, m, n$ 的交点个数为 0 或 1
已知椭圆 $C: \frac{x^2}{36}+\frac{y^2}{16}=1$ 上一点 $P$ 到左焦点 $F$ 的距离为 $8, O$ 为坐标原点, 若点 $M$ 满足 $\overrightarrow{O M}=\overrightarrow{O P}+\overrightarrow{O F}$, 则 $|\overrightarrow{O M}|=$
$\text{A.}$ 6
$\text{B.}$ 4
$\text{C.}$ $\frac{5}{2}$
$\text{D.}$ 2
已知函数 $f(x)=a \sin x+b \sqrt[3]{x}+c x^2 \tan x+4$, 且 $f\left(\lg \left(\log _3 5^{100}\right)\right)=6$, 则 $f\left(\lg \frac{\log _5 3}{100}\right)=$
$\text{A.}$ -6
$\text{B.}$ -2
$\text{C.}$ 2
$\text{D.}$ 4
多选题 (共 3 题 ),每题有多个选项正确
已知 $n \in N ^*$, 下列选项能正确表示数列 $1,0,1,0,1,0, \cdots$ 的公式有
$\text{A.}$ $ a_n=\frac{1-(-1)^{n+1}}{2}$
$\text{B.}$ $a_1=1, a_n+a_n=1$
$\text{C.}$ $a_n=\cos \frac{(n-1) \pi}{2}$
$\text{D.}$ $a_n=\left\{\begin{array}{l}1, n \text { 是奇数, } \\ 0, n \text { 是偶数 }\end{array}\right.$
已知函数 $f(x)= e ^x-a x+a^2$, 下列说法正确的有
$\text{A.}$ 对 $\forall a \in R$, 函数 $f(a) \geqslant a+1$
$\text{B.}$ 若函数 $f(x)$ 与 $g(x)=\ln x$ 的图象关于直线 $y=x$ 对称, 则 $a=0$
$\text{C.}$ 对 $\forall a \in R$, 函数 $f(x) \geqslant 0$
$\text{D.}$ 若 $\lim _{\Delta x \rightarrow 0} \frac{f(\Delta x)-a^2-1}{\Delta x}=0$, 则 $a=1$
如图, 曲线 $C$ 称为"双纽线", 其对称中心在坐标原点 $O$, 且 $C$ 上的点满足到点 $F_1(-a$, $0)$ 和 $F_2(a, 0)$ 的距离之积为定值 $a^2$, 则
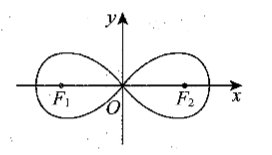
$\text{A.}$ 若 $a=1$, 点 $(\sqrt{2}, 0)$ 在曲线 $C$ 上
$\text{B.}$ 若 $a=1$, 曲线 $C$ 的方程为 $\left(x^2+y^2\right)^2=2 x^2-y^2$
$\text{C.}$ 若 $a=2$, 曲线 $C$ 上点的纵坐标的最大值为 1
$\text{D.}$ 若点 $\left(x_0, y_0\right)$ 在 $C$ 上, 则 $\left|y_0\right| \leqslant\left|x_0\right|$
填空题 (共 3 题 ),请把答案直接填写在答题纸上
已知 i 为虚数单位, 若复数 $(1- i )(1+a i )$ 是纯虚数,则实数 $a$ 的值为
《九章算术》第五章"商功"问题十七:今有羡除 ,下广六尺,上广一丈,深三尺,末广八尺, 无深, 衰七尺. 问积几何? 大意是:今有墓道(如图 (2),平面 $A B C D \perp$ 平面 $D C E F$ ),下宽( $A B$ 长) 6 尺,上宽( $C D$ 长) 1 丈( 1 丈 $=10$ 尺),深( $A B$ 与 $C D$ 距离) 3 尺,末端宽 ( $E F$ 长) 8 尺, 无深, 长 ( $E F$ 与 $C D$ 距离) 7 尺. 它的体积是 立方尺.

$\max _{x \in A}\{f(x, y)\}$ 表示函数 $f(x, y)$ 当自变量 $x \in A$ 时的最大值, $\min _{x \in A}\{f(x, y)\}$ 表示函数 $f(x, y)$ 当自变量 $x \in A$ 时的最小值,已知函数 $f(x, y)=-5 x y+\frac{5}{3}(x+y)-2$, 则 $\min _{x \in[0,1]}\left\{\max _{y \in[0,1]}\{f(x, y)\}\right\}=$ $\qquad$
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知函数 $f(x)=x^{--\frac{a(a-1)}{x}}-(2 a--1) \ln x-1$, 其中 $a \in R$.
(1) 若曲线 $y=f(x)$ 在点 $(1, f(1))$ 处与 $x$ 轴相切, 求 $a$ 的值;
(2) 若 3 是函数 $f(x)$ 的极小值点, 求 $a$ 的值.
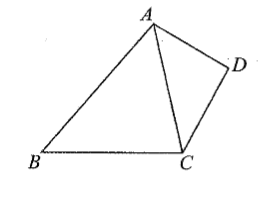
如图, 在四边形 $A B C D$ 中, $\angle A D C=2 \angle A B C$, 且 $A D=C D=2, \cos \angle A D C=\sin \angle C A D$ $-\cos \angle C A D$ 。
(1) 求 $\triangle A C D$ 的面积;
(2) 若 $B C=2 \sqrt{3}$, 求 $A B$ 的长.
已知椭圆 $E: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的长轴长是 $4, D$ 为右顶点, $P, Q, M, N$ 是椭圆 $E$ 上异于顶点的任意四个点, 当直线 $P Q$ 经过原点 $O$ 时, 直线 $P D$ 和 $Q D$ 的斜率之积为 $-\frac{1}{4}$.
(1) 求椭圆 $E$ 的方程;
(2) 当直线 $M D$ 和 $N D$ 的斜率之积为定值 -2 时, 直线 $M N$ 是否过一个定点? 若过定点, 求出该定点坐标; 若不过定点, 请说明理由.
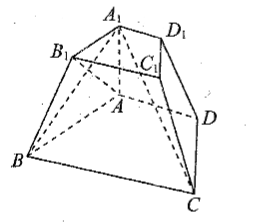
如图, 在四棱台 $A B C D-A_1 B_1 C_1 D_1$ 中, $A A_1 \perp$ 平面 $A B C D, A B_1 / /$ 平面 $C D D_1 C_1, A D / /$ $B C, A B=A D=C D=2 A A_1=2 A_1 B_1=2$.
(1) 求证: $A D=B_1 C_1$;
(2) 求平面 $C D D_1 C_1$ 与平面 $B A A_1 B_1$ 所成角的正弦值;
(3) 求点 $A$ 关于平面 $A_1 B C$ 的对称点 $M$ 到平面 $C D D_1 C_1$ 的距离.
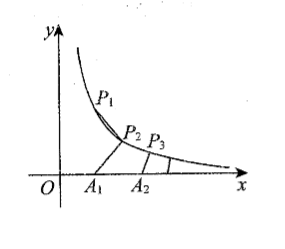
如图, 已知点列 $P_n\left(x_n, \frac{4}{x_n}\right)$ 与 $A_n\left(a_n, 0\right)$ 满足 $x_{n+1}>x_n, \overrightarrow{P_n P_{n+1}} \perp \overrightarrow{A_n P_{n+1}}$ 且 $\left|\overrightarrow{P_n P_{n+1}}\right|=$ $\left|\overrightarrow{A_n} \vec{P}_{n+1}\right|$, 其中 $n \in N ^*, x_1=\sqrt{2}$ 。
(1) 求 $x_{n+1}$ 与 $x_n$ 的关系式;
(2) 证明: $2 n^2+4 n+4 \leqslant x_1^2+x_2^2+x_3^2+\cdots+x_{n+1}^2 \leqslant 4 n^2+6 n$.