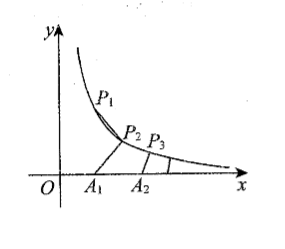
如图, 已知点列 $P_n\left(x_n, \frac{4}{x_n}\right)$ 与 $A_n\left(a_n, 0\right)$ 满足 $x_{n+1}>x_n, \overrightarrow{P_n P_{n+1}} \perp \overrightarrow{A_n P_{n+1}}$ 且 $\left|\overrightarrow{P_n P_{n+1}}\right|=$ $\left|\overrightarrow{A_n} \vec{P}_{n+1}\right|$, 其中 $n \in N ^*, x_1=\sqrt{2}$ 。
(1) 求 $x_{n+1}$ 与 $x_n$ 的关系式;
(2) 证明: $2 n^2+4 n+4 \leqslant x_1^2+x_2^2+x_3^2+\cdots+x_{n+1}^2 \leqslant 4 n^2+6 n$.