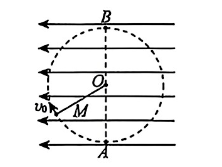
如图所示, 在水平向左且足够大的匀强电场中, 一长为 $L$ 的绝缘细线一端固定于 $O$ 点,另一端系着一个质是为 $m$ 、电荷量为 $q$ 的带正电小球,小球静置于 $M$ 点。现给小球一垂直于 $O M$ 向上的初速度 $v_0$, 使其在坚直平面内绕 $O$ 点恰好做完整的圆周运动, $A B$为圆的坚直直径。已知匀强电场的电场强度大小为 $\frac{\sqrt{3} m g}{q}$, 重力加速度为 $g$ 。当小球第二次运动到 $B$ 点时细线突然断裂, 则下列说法正确的是
A
小球做完整的圆周运动时, 动能的最小值为 $m g L$
B
小球第一次到 $B$ 点时, 细线上的力大小为 $4 m g$
C
细线断裂后,小球动能的最小值为 $\frac{1}{2} m g L$
D
从细线断裂到小球的电势能与在 $B$ 点时的电势能相等的过程中, 重力势能减少了 $\frac{8}{3} m g L$
E
F