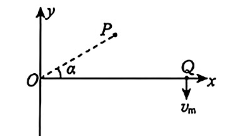
如图所示, 在 $x O y$ 平面内的第一象限内存在一有界匀强磁场（未画出）, 其磁感应强度大小为 $B$ 、方向垂直于 $x O y$ 平面向外。一束质量为 $m$ 、电荷量为 $+q$ 的粒子以不同的速率从 $O$ 点沿 $x O y$ 平面内的 $O P$ 方向发射, 粒子沿直线飞行到 $P$ 点时进入有界匀强磁场区域， $O 、 P$ 两点间的距离为 $L, O P$ 连线与 $x$ 轴正方向的夹角 $\alpha=30^{\circ}$ ，所有粒子在离开磁场后最终都能从 $x$ 轴上垂直 $x$ 轴射出，若速度最大的粒子 $A$ 从 $x$ 轴上的 $Q$ 点以速度 $v_{ m }$ (未知)射出,且射出之前始终在磁场内运动,粒子所受的重力忽略不计,求:
（1）最大速度 $v_{ m }$ 的大小；
（2）粒子 $A$ 在匀强磁场中运动的时间；
（3）有界匀强磁场区域的最小面积。