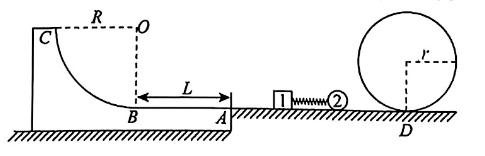
如图所示, 质量为 $2 m$ 的滑板上表面由长度为 $L$ 的水平部分 $A B$ 和半径为 $R$ 的四分之一光滑圆弧 $B C$ 组成，滑板静止在光滑的水平地面上， $A B$ 恰好与台阶等高。光滑的台阶上静置着质量均为 $m$ 的物块 1 和小球 2 ，两者之间有一被压缩的轻质弹簧。台阶右侧与一半径为 $r$ 的光滑固定坚直圆形轨道相切于 $D$ 点。某一时刻将压缩的弹簧释放，使得物块 1 与小球 2 瞬间分离，已知物块 1 向左运动的速度为 $v_0$ ，它与滑板水平部分的动摩擦因数为 $\mu$, 重力加速度为 $g$ 。
(1)若 $v_0=\sqrt{g r}$, 求小球 2 运动到 $D$ 点时, 圆形轨道所受压力的大小和方向;
(2) 为使小球 2 在运动过程中始终不脱离圆轨道,求圆形轨道的半径 $r$ 应满足的条件;
(3) 要使物块 1 在相对滑板反向运动的过程中, 相对地面有向右运动的速度, 求 $A B$ 的长度 $L$ 应满足的条件。