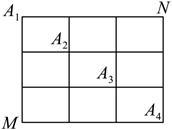
如图, 在某城市中, $M 、 N$ 两地之间有整齐的方格形道路网, 其中 $A_1 、 A_2 、 A_3 、 A_4$ 是道路网中位于一条对角线上的 4 个交汇处. 今在道路网 $M 、 N$ 处的甲、乙两人分别要到 $N 、 M$ 处, 他们分别随机地选择一条沿街的最短路径,以相同的速度同时出发,直到到达 $N 、 M$ 处为止.则下列说法正确的是
A
甲从 $M$ 到达 $N$ 处的方法有 120 种
B
甲从 $M$ 必须经过 $A_2$ 到达 $N$ 处的方法有 9 种
C
甲、乙两人在 $A_2$ 处相遇的概率为 $\frac{81}{400}$
D
甲、乙两人相遇的概率为 $\frac{41}{100}$
E
F