单选题 (共 1 题 ),每题只有一个选项正确
某校在校庆期间举办羽毛球比赛,某班派出甲、乙两名单打主力,为了提高两位主力的能力,体育老师安排了为期一周的对抗训练, 比赛规则如下: 甲、乙两人每轮分别与体育老师打 2 局, 当两人获胜局数不少于 3局时, 则认为这轮训练过关; 否则不过关.若甲、乙两人每局获胜的概率分别为 $p_1, p_2$, 且满足 $p_1+p_2=\frac{4}{3}$,每局之间相互独立. 记甲、乙在 $n$ 轮训练中训练过关的轮数为 $X$, 若 $E(X)=16$, 则从期望的角度来看, 甲、乙两人训练的轮数至少为()
$\text{A.}$ 27
$\text{B.}$ 24
$\text{C.}$ 32
$\text{D.}$ 28
多选题 (共 5 题 ),每题有多个选项正确
随着春节的临近,小王和小张等 4 位同学准备互相送祝福。他们每人写了一个祝福的贺卡,这四张贺卡收齐后让每人从中随机抽取一张作为收到的新春祝福, 则()
$\text{A.}$ 小王和小张恰好互换了贺卡的概率为 $\frac{1}{6}$
$\text{B.}$ 已知小王抽到的是小张写的贺卡的条件下, 小张抽到小王写的贺卡的概率为 $\frac{1}{3}$
$\text{C.}$ 恰有一个人抽到自己写的贺卡的概率为 $\frac{1}{3}$
$\text{D.}$ 每个人抽到的贺卡都不是自己写的概率为 $\frac{5}{8}$
设 $A , B$ 是一个随机试验中的两个事件, 且 $P(A)=\frac{1}{3}, P(B)=\frac{3}{4}, P(A+\bar{B})=\frac{1}{2}$, 则 ( )
$\text{A.}$ $P(A \bar{B})=\frac{1}{6}$
$\text{B.}$ $P(B \mid A)=\frac{3}{4}$
$\text{C.}$ $P(\bar{B})=P(\bar{B} \mid A)$
$\text{D.}$ $P(A \bar{B}+\bar{A} B)=\frac{7}{12}$
如图, 在某城市中, $M 、 N$ 两地之间有整齐的方格形道路网, 其中 $A_1 、 A_2 、 A_3 、 A_4$ 是道路网中位于一条对角线上的 4 个交汇处. 今在道路网 $M 、 N$ 处的甲、乙两人分别要到 $N 、 M$ 处, 他们分别随机地选择一条沿街的最短路径,以相同的速度同时出发,直到到达 $N 、 M$ 处为止.则下列说法正确的是
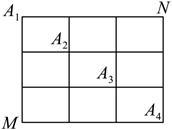
$\text{A.}$ 甲从 $M$ 到达 $N$ 处的方法有 120 种
$\text{B.}$ 甲从 $M$ 必须经过 $A_2$ 到达 $N$ 处的方法有 9 种
$\text{C.}$ 甲、乙两人在 $A_2$ 处相遇的概率为 $\frac{81}{400}$
$\text{D.}$ 甲、乙两人相遇的概率为 $\frac{41}{100}$
十七世纪至十八世纪的德国数学家莱布尼兹是世界上第一个提出二进制记数法的人, 用二进制记数只需数字 0 和 1 , 对于整数可理解为逢二进, 例如: 自然数 1 在二进制中就表示为 1,2 表示为 10,3 表示为 11 , 7 表示为 111 , 即 $n \in N _{+}, n=a_0 \cdot 2^k+a_1 \cdot 2^{k-1}+ L +a_{k-1} \cdot 2^1+a_k$, 其中 $a_0=1, a_i=0$ 或 $1(i=1,2, L, k)$, 记 $I(n)$为上述表示中 0 的个数,如 $I(2)=1, I(7)=0$ 。则下列说法中正确的是().
$\text{A.}$ $I(12) < I(18)$
$\text{B.}$ $I\left(2^k-2\right)-I\left(2^k-1\right)=1\left(k \in N _{+}, k \geq 2\right)$
$\text{C.}$ $I(2 k)=I(2 k+2)\left(k \in N _{+}\right)$
$\text{D.}$ 1 到 127 这些自然数的二进制表示中 $I(n)=2$ 的自然数有 35 个
某人投了 100 次篮, 设投完前 $n$ 次的命中率为 $r_m$. 其中 $n=1,2, \ldots .100$. 已知 $r_1=0, r_{100}=0.85$, 则一定存在 $0 < m < 100$ 使得()
$\text{A.}$ $r_m=0.5$
$\text{B.}$ $r_m=0.6$
$\text{C.}$ $r_m=0.7$
$\text{D.}$ $r_m=0.8$