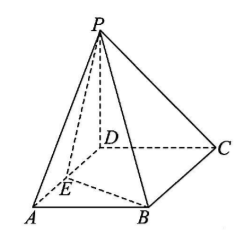
已知两个非零向量 $\vec{a}, \vec{b}$ ，在空间任取一点 $O$ ，作 $\overrightarrow{O A}=\vec{a}, \overrightarrow{O B}=\vec{b}$ ，则 $\angle A O B$ 叫做向量 $\vec{a}, \vec{b}$ 的夹角，记作 $\langle\vec{a}, \vec{b}\rangle$ ．定义 $\vec{a}$ 与 $\vec{b}$ 的＂向量积＂为：$\vec{a} \times \vec{b}$ 是一个向量，它与向量 $\vec{a}, \vec{b}$ 都垂直，它的模 $|\vec{a} \times \vec{b}|=|\vec{a}| \cdot|\vec{b}| \sin \langle\vec{a}, \vec{b}\rangle$ ．如图，在四棱锥 $P-A B C D$ 中，底面 $A B C D$ 为矩形，$P D \perp$ 底面 $A B C D$ ， $D P=D A=4, E$ 为 $A D$ 上一点，$|\overrightarrow{A D} \times \overrightarrow{B P}|=8 \sqrt{5}$ ．
（1）求 $A B$ 的长；
（2）若 $E$ 为 $A D$ 的中点，求二面角 $P-E B-A$ 的余弦值；
（3）若 $M$ 为 $P B$ 上一点，且满足 $\overrightarrow{A D} \times \overrightarrow{B P}=\lambda \overrightarrow{E M}$ ，求 $|\lambda|$ ．