单选题 (共 11 题 ),每题只有一个选项正确
若随机变量 $X \sim N(6,1)$ ,且 $P(5 < X \leq 7)=a, P(4 < X \leq 8)=b$ ,则 $P(4 < X \leq 7)$ 等于
$\text{A.}$ $\frac{b-a}{2}$
$\text{B.}$ $\frac{b+a}{2}$
$\text{C.}$ $\frac{1-b}{2}$
$\text{D.}$ $\frac{1-a}{2}$
底面边长为 4 的正四棱锥被平行于其底面的平面所截,截去一个底面边长为 1 ,高为 1的正四棱锥,所得棱台的体积为()
$\text{A.}$ 18
$\text{B.}$ 21
$\text{C.}$ 54
$\text{D.}$ 63
设圆 $C_1: x^2+y^2-10 x+4 y+25=0$ 与圆 $C_2: x^2+y^2-6 x+8=0$ ,点 $A, B$ 分别是 $C_1$ , $C_2$ 上的动点,$M$ 为直线 $y=x+1$ 上的动点,则 $|M A|+|M B|$ 的最小值为()
$\text{A.}$ $2 \sqrt{2}+3$
$\text{B.}$ $3-2 \sqrt{2}$
$\text{C.}$ $6 \sqrt{2}-3$
$\text{D.}$ $6 \sqrt{2}+3$
已知直线 $l_1: m x+y+3=0$ 和直线 $l_2: 3 m x+(m-2) y+m=0$ ,则"$m=5$"是"$l_1 \| l_2$"的()
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分也不必要条件
某单位春节共有四天假期,但每天都需要留一名员工值班,现从甲,乙,丙,丁,戊,己六人选出四人值班,每名员工最多值班一天,已知甲在第一天不值班,乙在第四天不值班,则值班安排共有( )
$\text{A.}$ 192 种
$\text{B.}$ 252 种
$\text{C.}$ 268 种
$\text{D.}$ 360 种
设 $\triangle A B C$ 的三个顶点为复平面上的三点 $z_1, z_2, z_3$ ,满足 $z_1 z_2 z_3=0, z_1+z_2+z_3=8+2 i$ , $z_1 z_2+z_2 z_3+z_1 z_3=15+10 i$ ,则 $\triangle A B C$ 内心的复数坐标 $z$ 的虚部所在区间是().
$\text{A.}$ $(0.5,1)$
$\text{B.}$ $(0,0.5)$
$\text{C.}$ $(1,2)$
$\text{D.}$ 前三个选项都不对
$\triangle A B C$ 的内角 $A, B, C$ 的对边分别为 $a, b, c$ ,已知 $c=2, \frac{\sin C}{\cos C}=\frac{\sin A}{2-\cos A}, M$ 和 $N$ 分别是 $\triangle A B C$ 的重心和内心,且 $M N / / B C$ ,则 $a=$( )
$\text{A.}$ 2
$\text{B.}$ 3
$\text{C.}$ 4
$\text{D.}$ 6
正整数 $a, b, c \in\{1,2, \cdots, 100\}$ ,且 $\frac{1}{a}+\frac{1}{c}=\frac{2}{b}, a>b>c$ ,满足这样条件的 $(a, b, c)$ 的组数为
$\text{A.}$ 60
$\text{B.}$ 90
$\text{C.}$ 75
$\text{D.}$ 86
已知 $x_1, x_2$ ,是函数 $f(x)=\tan (\omega x+\varphi)(\omega>0,-\pi < \varphi < \pi)$ 的两个零点,且 $\left|x_1-x_2\right|$ 的最小值为 $\frac{\pi}{3}$ ,若将函数 $f(x)$ 的图象向左平移 $\frac{\pi}{12}$ 个单位长度后得到的图象关于原点对称,则 $\varphi$ 的可能值为()
$\text{A.}$ $\frac{3 \pi}{4}$
$\text{B.}$ $\frac{\pi}{4}$
$\text{C.}$ $-\frac{\pi}{4}$
$\text{D.}$ $\frac{\pi}{8}$
曲线 $C$ 的方程为 $\frac{x^4}{a^4}+\frac{y^4}{b^4}=1(a>0, b>0)$ ,下列对曲线 $C$ 的描述正确的是
$\text{A.}$ 曲线 $C$ 关于原点对称
$\text{B.}$ 曲线 $C$ 与椭圆 $C^{\prime}: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>0, b>0)$ 无公共点
$\text{C.}$ 曲线 $C$ 所围成的封闭图形的面积大于椭圆 $C^{\prime}: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>0, b>0)$ 围成的封闭图形的面积
$\text{D.}$ 曲线 $C$ 上的点到原点距离的最大值为 $a$
在棱长为 2 的正方体 $A B C D-A_1 B_1 C_1 D_1$ 中,$Q$ 是 $C C_1$ 的中点,下列说法正确的是
$\text{A.}$ 若 $P$ 是线段 $A C_1$ 上的动点,则三棱锥 $P-B Q D$ 的体积为定值
$\text{B.}$ 三棱锥 $A_1-B Q D$ 外接球的半径为 $\frac{\sqrt{66}}{6}$
$\text{C.}$ 若 $A Q$ 与平面 $A C$ ,平面 $A D_1$ ,平面 $A B_1$ 所成的角分别为 $\theta_i(i=1,2,3)$ ,则 $\sum_{i=1}^3 \cos ^2 \theta_i=2$
$\text{D.}$ 若平面 $A B Q$ 与正方体各个面所在的平面所成的二面角分别为 $\theta_i(i=1, \cdots, 6)$ ,则 $\sum_{i=1}^6 \sin ^2 \theta_i=4$
填空题 (共 3 题 ),请把答案直接填写在答题纸上
曲线 $y=|\ln x|$ 在 $A\left(x_1, y_1\right), B\left(x_2, y_2\right)$ 两点处的切线分别为 $l_1, l_2$ ,且 $l_1 \perp l_2$ ,则 $x_1 x_2=$ $\qquad$ ;若 $l_1, l_2$ 交点的横坐标为 $x_3$ ,则 $x_1 x_3+x_2 x_3=$ $\qquad$ .(第一空 2 分,第二空 3 分)
设函数 $f(x)=a^x+b^x-c^x$ ,其中 $a, b, c$ 是 $\triangle A B C$ 的三条边长,且有 $c>a, c>b$ .给出下列四个结论:
(1)若 $a=b$ ,则 $f(x)$ 的零点均大于 1 ;
(2)若 $a=2, b=3, c=4$ ,则对任意 $x \in(0,+\infty), a^x, b^x, c^x$ 都能构成一个三角形的三条边长;
(3)对任意 $x \in(-\infty, 1], f(x)>0$ ;
(4)若 $\triangle A B C$ 为直角三角形,则对任意 $n \in N^*, f(2 n) \leqslant 0$ .其中所有正确结论的序号是
设 $a, b>0$ ,满足:关于 $x$ 的方程 $\sqrt{|x|}+\sqrt{|x+a|}=b$ 恰有三个不同的实数解 $x_1, x_2, x_3$ ,且 $x_1 < x_2 < x_3=b$ ,则 $a+b$ 的值为 $\qquad$ .
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知圆 $C:(x+4)^2+y^2=1$ 和点 $A(1,0), P$ 为圆 $C$ 外一点,直线 $P Q$ 与圆 $C$ 相切于点 $Q, P Q=$ $\sqrt{2} P A$
(1)求点 $P$ 的轨迹方程;
(2)记(1)中的点 $P$ 的轨迹为 $T$ ,是否存在斜率为 -1 的直线 $l$ ,使以 $l$ 被曲线 $T$ 截得得弦 $M N$ 为直径得圆过点 $B(-2,0)$ ?若存在,求出直线 $l$ 的方程;若不存在,说明理由.
随着"双十一购物节"的来临,某服装店准备了抽奖活动回馈新老客户,活动规则如下:奖券共 3 张,分别可以再店内无门槛优惠 10 元, 20 元和 30 元,每人每天可抽 1 张奖券,每人抽完后将所抽取奖券放回,以供下一位顾客抽取.若某天抽奖金额少于 20 元,则下一天可无放回地抽 2 张奖券,以优惠金额更大的作为所得,否则正常抽取.
(1)求第二天获得优惠金额的数学期望;
(2)记"第 $i$ 天抽取 1 张奖券"的概率为 $P_i$ ,写出 $P_i$ 与 $P_{i+1}$ 的关系式并求出 $P_i$ .
已知函数 $f(x)=(x-2) e ^x, g(x)=2 x^3-3 x^2$ .
(1)求曲线 $f(x)$ 在 $(1, f(1))$ 处的切线方程;
(2)已知实数 $a>0$ ,设 $h(x)=a f(x)-g(x)$ .
(i)若 $a=3$ ,求 $h(x)$ 的极值;
(ii)若 $h(x)$ 有 3 个零点,求 $a$ 的值.
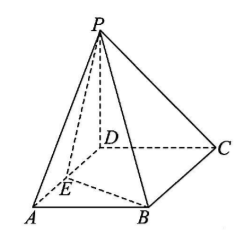
已知两个非零向量 $\vec{a}, \vec{b}$ ,在空间任取一点 $O$ ,作 $\overrightarrow{O A}=\vec{a}, \overrightarrow{O B}=\vec{b}$ ,则 $\angle A O B$ 叫做向量 $\vec{a}, \vec{b}$ 的夹角,记作 $\langle\vec{a}, \vec{b}\rangle$ .定义 $\vec{a}$ 与 $\vec{b}$ 的"向量积"为:$\vec{a} \times \vec{b}$ 是一个向量,它与向量 $\vec{a}, \vec{b}$ 都垂直,它的模 $|\vec{a} \times \vec{b}|=|\vec{a}| \cdot|\vec{b}| \sin \langle\vec{a}, \vec{b}\rangle$ .如图,在四棱锥 $P-A B C D$ 中,底面 $A B C D$ 为矩形,$P D \perp$ 底面 $A B C D$ , $D P=D A=4, E$ 为 $A D$ 上一点,$|\overrightarrow{A D} \times \overrightarrow{B P}|=8 \sqrt{5}$ .
(1)求 $A B$ 的长;
(2)若 $E$ 为 $A D$ 的中点,求二面角 $P-E B-A$ 的余弦值;
(3)若 $M$ 为 $P B$ 上一点,且满足 $\overrightarrow{A D} \times \overrightarrow{B P}=\lambda \overrightarrow{E M}$ ,求 $|\lambda|$ .
桌上有十个苹果,要把这十个苹果放到九个抽屉里,无论怎样放,我们会发现至少会有一个抽屉里面放不少于两个苹果。这一现象就是我们所说的"抽屉原理"。
抽屉原理的一般含义为:如果每个抽屉代表一个集合,每一个苹果就可以代表一个元素,假如有 $n+1$ 个元素放到 $n$ 个集合中去,其中必定有一个集合里至少有两个元素。
应用抽屉原理,解答下列问题:设 $n$ 为正整数,集合 $A=\left\{\alpha \mid \alpha=\left(t_1, t_2, \cdots, t_n\right), t_k \in\{0,1\}, k=1\right.$ , $2, \cdots, n\}$ .对于集合 $A$ 中的任意元素 $\alpha=\left(x_1, x_2, \cdots, x_n\right)$ 和 $\beta=\left(y_1, y_2, \cdots, y_n\right)$ ,记 $M(\alpha, \beta)=$ $\frac{1}{2}\left[\left(x_1+y_1+\left|x_1-y_1\right|\right)+\left(x_2+y_2+\left|x_2-y_2\right|\right)+\cdots+\left(x_n+y_n+\left|x_n-y_n\right|\right)\right]$ .
(I)当 $n=3$ 时,若 $\alpha=(0,1,1), \beta=(0,0,1)$ ,求 $M(\alpha, \alpha)$ 和 $M(\alpha, \beta)$ 的值;
(II)当 $n=4$ 时,对于 $A$ 中的任意两个不同的元素 $\alpha, \beta$ ,证明:$M(\alpha, \beta) \leq M(\alpha, \alpha)+M(\beta, \beta)$ .
(III)给定不小于 2 的正整数 $n$ ,设 $B$ 是 $A$ 的子集,且满足:对于 $B$ 中的任意两个不同元素 $\alpha, \beta, M(\alpha, \beta)=M(\alpha, \alpha)+M(\beta, \beta)$ .写出一个集合 $B$ ,使其元索个数最多,并说明由.