某大学排球社团为了解性别因索是否对学生喜欢排球有影响，随机调查了男，女生各 200 名，得到如下数据：

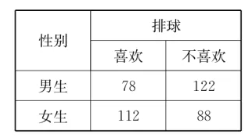
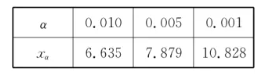
（1）依据小概率值 $\alpha=0.001$ 的独立性检验，能否认为是否喜欢排球与性别有关联？
（2）在某次社团活动中，甲，乙，丙这三人相互做传球训练，第 1 次由甲将球传出，每次传球时，传球者都等可能地将球传给另外两个人中的任何一人．记 $n$ 次传球后球在乙手中的概率为 $p_n, n=1,2,3, \cdots$ ．
（i）求 $p_n$ ；
（ii）若随机变量 $X_i$ 服从两点分布，且 $P\left(X_i=1\right)=1-P\left(X_i=0\right)=q_i, i=1,2, \cdots, n$ ，则 $E\left(\sum_{i=1}^n X_i\right)$ $=\sum_{i=1}^n q_i$ ．记前 $n$ 次（即从第 1 次到第 $n$ 次传球）中球在乙手中的次数为随机变量 $Y$ ，求 $Y$ 的数学期望。
附：$\chi^2=\frac{n(a d-b c)^2}{(a+b)(c+d)(a+c)(b+d)}$ ，其中 $n=a+b+c+d$ ．