填空题 (共 2 题 ),请把答案直接填写在答题纸上
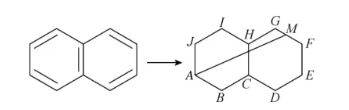
键线式可以简洁直观地描述有机物的结构,在有机化学中极其重要.有机物萘可以用如图所示的键线式表示,其结构简式可以抽象为右图所示的图形.已知六边形 $A B C H I J$ 与六边形 $C D E F G H$ 为全等的正六边形,且 $A B=4$ ,点 $M$ 为正六边形 $C D E F G H$ 内的一点(包含边界),则 $\overrightarrow{A B} \cdot \overrightarrow{A M}$ 的取值范围是
柯西不等式(Cauchy-SchwarzLnequality)是法国数学家柯西与德国数学家施瓦茨分别独立发现的,它在数学分析中有广泛的应用.现给出一个二维柯西不等式:$\left(a^2+b^2\right)\left(c^2+d^2\right) \geqslant(a c+b d)^2$ ,当且仅当 $a d=b c$ 时等号成立.已知 $a>0, b>0$ ,直线 $y=x-2 a$ 与曲线 $y=\ln (x+b)$ 相切,则 $\frac{1}{a}+\frac{1}{b}+\sqrt{\frac{1}{a^2}+\frac{1}{b^2}}$的最小值为
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
记 $\triangle A B C$ 的内角 $A, B, C$ 的对边分别为 $a, b, c$ ,且 $2 a \cos A+b \cos C=c \cos (A+C)$ .
(1)求角 $A$ 的大小;
(2)若 $a=\sqrt{21}, B C$ 边上的高为 $\frac{2 \sqrt{7}}{7}$ ,求 $\triangle A B C$ 的周长.
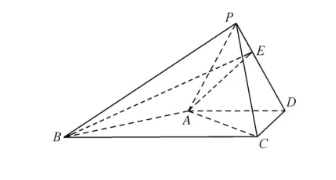
如图,在四棱锥 $P-A B C D$ 中,$\triangle P A D$ 是边长为 2 的等边三角形,$C A=C P=2 \sqrt{2}, B C=4, A D / / B C$ ,点 $E$ 是棱 $P D$ 上的一点,且满足 $D E=2 E P, A E \perp D C$ .
(1)求证:平面 $P A D \perp$ 平面 $A B C D$ ;
(2)求平面 $A B E$ 与平面 $P B C$ 的夹角的余弦值.
已知函数 $f(x)=(a x+1) e ^x-1(a \in R )$ .
(1)若 $a=-2$ ,求 $f(x)$ 的极值;
(2)若 $f(x) \leqslant(a+1) x$ 对任意的 $x \in[0,+\infty)$ 恒成立,求 $a$ 的取值范围.
某大学排球社团为了解性别因索是否对学生喜欢排球有影响,随机调查了男,女生各 200 名,得到如下数据:
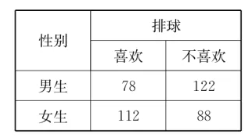
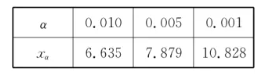
(1)依据小概率值 $\alpha=0.001$ 的独立性检验,能否认为是否喜欢排球与性别有关联?
(2)在某次社团活动中,甲,乙,丙这三人相互做传球训练,第 1 次由甲将球传出,每次传球时,传球者都等可能地将球传给另外两个人中的任何一人.记 $n$ 次传球后球在乙手中的概率为 $p_n, n=1,2,3, \cdots$ .
(i)求 $p_n$ ;
(ii)若随机变量 $X_i$ 服从两点分布,且 $P\left(X_i=1\right)=1-P\left(X_i=0\right)=q_i, i=1,2, \cdots, n$ ,则 $E\left(\sum_{i=1}^n X_i\right)$ $=\sum_{i=1}^n q_i$ .记前 $n$ 次(即从第 1 次到第 $n$ 次传球)中球在乙手中的次数为随机变量 $Y$ ,求 $Y$ 的数学期望。
附:$\chi^2=\frac{n(a d-b c)^2}{(a+b)(c+d)(a+c)(b+d)}$ ,其中 $n=a+b+c+d$ .
椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的"特征三角形".记椭圆 $C_1$ 的"特征三角形"为 $\triangle_1$ ,椭圆 $C_2$ 的"特征三角形"为 $\triangle_2$ ,若 $\triangle_1 \backsim \triangle_2$ ,则称椭圆 $C_1$ 与 $C_2$ 相似,并将 $\triangle_1$ 与 $\triangle_2$ 的相似比称为椭圆 $C_1$ 与 $C_2$ 的相似比.已知椭圆 $C_1: \frac{x^2}{8}+\frac{y^2}{4}=1$ 与椭圆 $C_2: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 相似,且 $C_1$ 与 $C_2$ 的相似比为 2 .
(1)求 $C_2$ 的方程;
(2)已知点 $F$ 是 $C_2$ 的右焦点,过点 $F$ 的直线 $l$ 与 $C_1$ 交于 $A, B$ 两点,直线 $l$ 与 $C_2$ 交于 $D, E$ 两点,其中点 $D$ 在 $x$ 轴上方.
(i)求证:$|A D|=|B E|$ ;
(ii)若过点 $F$ 与直线 $l$ 垂直的直线交 $C_2$ 于 $G, H$ 两点,其中点 $G$ 在 $x$ 轴上方,$M, N$ 分别为 $D E$ , $G H$ 的中点,设 $P$ 为直线 $G D$ 与直线 $E H$ 的交点,求 $\triangle P M N$ 面积的最小值.