在 $\triangle A B C$ 中，角 $A, B, C$ 的对边分别是 $a, b, c$ ，且满足 $\sin ^{2} B+\sin ^{2} C-\sin B \sin C=\sin ^{2} A$ ．

（1）求角 $A$ ；
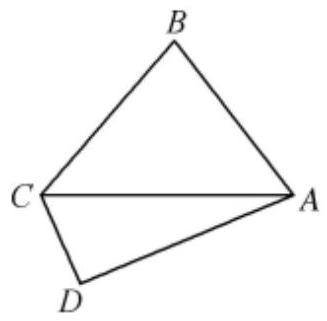
（2）如图，若 $b=c$ ，点 $D$ 是 $\triangle A B C$ 外一点，$D A=3, D C=\sqrt{3}$ ，设 $\angle A D C=\theta$ ，求平面四边形 $A B C D$ 面积的最大值及相应的 $\theta$ 值．