单选题 (共 7 题 ),每题只有一个选项正确
为了在一条河上建一座桥,施工前在河两岸打上两个桥位桩 $A, B$(如图),要测量 $A, B$ 两点的距离,测量人员在岸边定出基线 $AC$ ,测得 $B C=50 \mathrm{~m}, \angle A B C=105^{\circ}, \angle B C A=45^{\circ}$ .就可以计算出 $A, B$ 两点的距离为
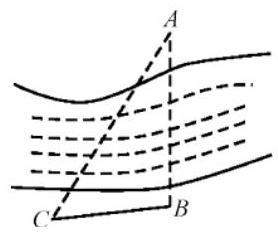
$\text{A.}$ $20 \sqrt{2} m$
$\text{B.}$ $30 \sqrt{2} \mathrm{~m}$
$\text{C.}$ $40 \sqrt{2} \mathrm{~m}$
$\text{D.}$ $50 \sqrt{2} m$
已知 $\triangle A B C$ 的面积 $S=\frac{1}{4}\left(a^{2}+b^{2}-c^{2}\right)$ ,则角 $C$ 的大小为
$\text{A.}$ $135^{\circ}$
$\text{B.}$ $45^{\circ}$
$\text{C.}$ $60^{\circ}$
$\text{D.}$ $120^{\circ}$
一块形状近似为三角形的草坪,若其中两角的正切值分别为 $\frac{1}{4}$ 与 $\frac{3}{5}$ ,且最长的边为 $\sqrt{17} \mathrm{~m}$ ,则最短的边为( )
$\text{A.}$ $\sqrt{3} \mathrm{~m}$
$\text{B.}$ $2 \sqrt{3} \mathrm{~m}$
$\text{C.}$ $\sqrt{2} \mathrm{~m}$
$\text{D.}$ 5 m
如图,有一壁画,最高点 $A$ 处离地面 12 m ,最低点 $B$ 处离地面 7 m .若从离地高 4 m 的 $C$ 处观赏它,若要视角 $\theta$ 最大,则离墙的距离为
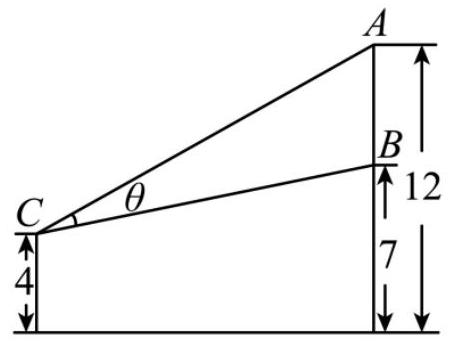
$\text{A.}$ $\sqrt{6} m$
$\text{B.}$ 3 m
$\text{C.}$ 4 m
$\text{D.}$ $2 \sqrt{6} m$
在 $\triangle A B C$ 中,$A C=2 \sqrt{2}, B C=4$ ,则角 $B$ 的最大值为 ()
$\text{A.}$ $\frac{\pi}{4}$
$\text{B.}$ $\frac{\pi}{3}$
$\text{C.}$ $\frac{\pi}{2}$
$\text{D.}$ $\frac{\pi}{6}$
如图,$\triangle A B C$ 中,角 $C$ 的平分线 $C D$ 交边 $A B$ 于点 $D, \angle A=\frac{2 \pi}{3}, A C=2 \sqrt{3}, C D=3 \sqrt{2}$ ,则 $B C=$
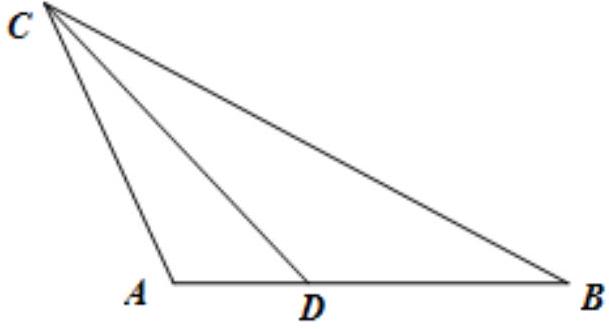
$\text{A.}$ $3 \sqrt{3}$
$\text{B.}$ 4
$\text{C.}$ $4 \sqrt{2}$
$\text{D.}$ 6
在锐角三角形 $A B C$ 中,已知 $a, b, c$ 分别是角 $A, B, C$ 的对边,且 $\sqrt{3} b=2 a \sin B, a=6$ ,则 $b+c$ 的取值范围是
$\text{A.}$ $[6,12]$
$\text{B.}$ $(6,12]$
$\text{C.}$ $(6 \sqrt{3}, 12]$
$\text{D.}$ $[6 \sqrt{3}, 12]$
填空题 (共 1 题 ),请把答案直接填写在答题纸上
在 $\triangle A B C$ 中,$a, b, c$ 分别是内角 $A, B, C$ 的对边,且 $B$ 为锐角,若 $\frac{\sin A}{\sin B}=\frac{5 c}{2 b}, \sin B=\frac{\sqrt{7}}{4}, S_{\triangle A B C}=\frac{5 \sqrt{7}}{4}$ ,则 $b$ 的值为 $\qquad$ .
解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
记 $\triangle A B C$ 的内角 $A, B, C$ 的对边分别为 $a, b, c$ ,已知 $\triangle A B C$ 面积为 $\sqrt{3}$ ,若 $D$ 为 $B C$ 中点,且 $A D=1$ .
(1)若 $\angle A D C=\frac{\pi}{3}$ ,求 $\tan B$ ;
(2)若 $b^{2}+c^{2}=8$ ,求 $b, c$ .
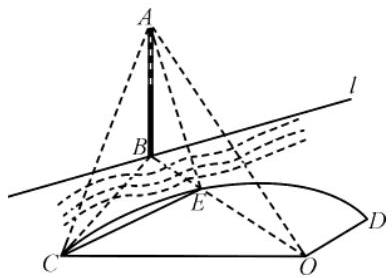
如图,有一段河流,河的一侧是以 $O$ 为圆心,半径为 $10 \sqrt{3} \mathrm{~m}$ 的扇形区域 $O C D$ ,河的另一侧是一段笔直的河岸 $l$ ,岸边有一烟囱 $A B$(不计 $B$ 离河岸的距离),且 $O B$ 的连线恰好与河岸 $l$ 垂直,设 $O B$ 与圆弧的交点为 $E$ .经测量,扇形区域和河岸处于同一水平面,在点 $C$ ,点 $O$ 和点 $E$ 处测得烟囱 $A B$ 的仰角分别为 $45^{\circ}$ , $30^{\circ}$ 和 $60^{\circ}$ 。
(1)求烟囱 $A B$ 的高度;
(2)如果要在 $C E$ 间修一条直路,求 $C E$ 的长.
已知 $\triangle A B C$ 的内角 $A, B, C$ 的对边分别为 $a, b, c$ ,且满足 $(a-c)(\sin A+\sin C)-\sin B \cdot(a-b)=0$ .
(1)求 $C$ ;
(2)若 $S_{\triangle A B C}=2 \sqrt{3}, D$ 为边 $A B$ 的中点,求 $C D$ 的最小值.
已知在四边形 $A B C D$ 中,$A B=7, B C=13, C D=A D$ ,且 $\cos B=\frac{1}{7}, \angle B A D=2 \angle B C D$ .
(1)求 $\angle B C A$ ;
(2)求 $A D$ .
在 $\triangle A B C$ 中,角 $A, B, C$ 的对边分别是 $a, b, c$ ,且满足 $\sin ^{2} B+\sin ^{2} C-\sin B \sin C=\sin ^{2} A$ .
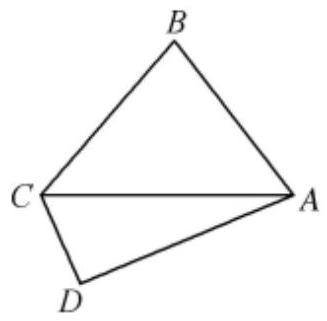
(1)求角 $A$ ;
(2)如图,若 $b=c$ ,点 $D$ 是 $\triangle A B C$ 外一点,$D A=3, D C=\sqrt{3}$ ,设 $\angle A D C=\theta$ ,求平面四边形 $A B C D$ 面积的最大值及相应的 $\theta$ 值.
某校数学建模社团学生为了测量该校操场旗杆的高 $A B$ ,先在旗杆底端的正西方点 $C$ 处测得杆顶的仰角为 $45^{\circ}$ ,然后从点 $C$ 处沿南偏东 $30^{\circ}$ 方向前进 20 m 到达点 $D$ 处,在 $D$ 处测得杆顶的仰角为 $30^{\circ}$ ,则旗杆的高为( )
A. 20 m
B. 10 m
C. $10 \sqrt{3} \mathrm{~m}$
D.$\frac{10 \sqrt{3}}{3} \mathrm{~m}$
在 $\triangle A B C$ 中,角 $A, B, C$ 的对边分别是 $a, b, c$ ,且满足 $\sin ^{2} B+\sin ^{2} C-\sin B \sin C=\sin ^{2} A$ .
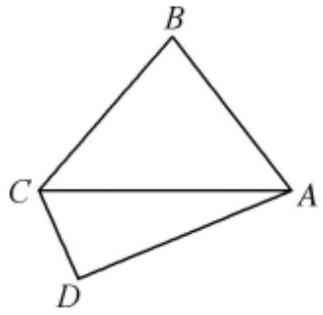
(1)求角 $A$ ;
(2)如图,若 $b=c$ ,点 $D$ 是 $\triangle A B C$ 外一点,$D A=3, D C=\sqrt{3}$ ,设 $\angle A D C=\theta$ ,求平面四边形 $A B C D$ 面积的最大值及相应的 $\theta$ 值.