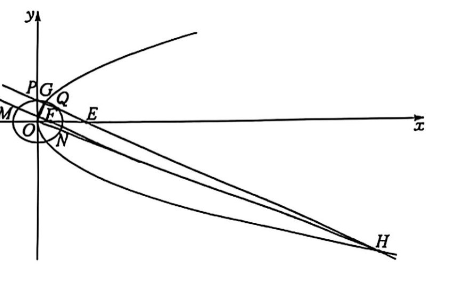
已知椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 及抛物线 $D: y^2=2 p x(p>0)$ 都经过点 $A\left(\frac{2}{3}, \frac{2 \sqrt{6}}{3}\right)$ ，且 $C$ 的右焦点与 $D$ 的焦点 $F$ 重合．
（1）求 $C$ 与 $D$ 的方程；
（2）过点 $E(2 p, 0)$ 作直线与 $C$ 交于 $P, Q$ 两点，与 $D$ 交于 $G, H$ 两点，过点 $F$ 作直线 $P Q$ 的平行线与 $C$交于 $M, N$ 两点．
（ 1 ）已知 $O$ 为原点，证明：$O G \perp O H$ ；
（II）判断是否存在常数 $k$ ，使得 $\overrightarrow{E P} \cdot \overrightarrow{E Q}+k \overrightarrow{F M} \cdot \overrightarrow{F N}=0$ ，并证明你的结论．