单选题 (共 8 题 ),每题只有一个选项正确
已知集合 $A=\{-3,-1,0,1,3\}, B=\left\{x \left\lvert\, y=\frac{x}{\sqrt{x+1}}\right.\right\}$ ,则 $A \cap B=$
$\text{A.}$ $\{0,1,3\}$
$\text{B.}$ $\{-1,0,1,3\}$
$\text{C.}$ $\{1,3\}$
$\text{D.}$ $\{-3,-1\}$
若复数 $1+(a-\sqrt{2} i )^2(a \in R )$ 为纯虚数,则 $a=$
$\text{A.}$ 1
$\text{B.}$ $\sqrt{2}$
$\text{C.}$ $\pm 1$
$\text{D.}$ $\pm \sqrt{2}$
已知某地 3 月 $\sim 5$ 月份的日平均气温 $X$(单位:${ }^{\circ} C$ )服从正态分布 $N\left(15, \sigma^2\right)$ ,若 $P(X \leqslant 14)=0.3$ ,则 $P(14 < X < 16)=$
$\text{A.}$ 0.2
$\text{B.}$ 0.4
$\text{C.}$ 0.6
$\text{D.}$ 0.7
若向量 $a =(1, m), b =(2,-1)$ ,且 $a \perp b$ ,则 $\cos \langle a - b , b \rangle=$
$\text{A.}$ $\frac{\sqrt{2}}{10}$
$\text{B.}$ $\frac{\sqrt{2}}{2}$
$\text{C.}$ $-\frac{\sqrt{2}}{10}$
$\text{D.}$ $-\frac{\sqrt{2}}{2}$
已知 $a=\log _2 3-\log _3 5, b=\log _5 7-\log _7 9$ ,则
$\text{A.}$ $a>0, b>0$
$\text{B.}$ $a>0, b < 0$
$\text{C.}$ $a < 0, b>0$
$\text{D.}$ $a < 0, b < 0$
已知函数 $f(x)= e ^{-2 x}+a x^2$ 恰有两个极值点,则实数 $a$ 的取值范围是
$\text{A.}$ $(-\infty,- e )$
$\text{B.}$ $(-\infty,-2 e )$
$\text{C.}$ $(-2 e , 0)$
$\text{D.}$ $(-\infty,-2 e ) \cup(0,+\infty)$
已知点 $A, B$ 是圆 $C: x^2+y^2-8 y+12=0$ 上的两个动点,$O$ 为原点,点 $A, B, O$ 共线,点 $D$ 为 $A B$ 的中点,则点 $D$ 的轨迹长度为
$\text{A.}$ $\frac{8 \pi}{3}$
$\text{B.}$ $2 \pi$
$\text{C.}$ $\frac{4 \pi}{3}$
$\text{D.}$ $\frac{2 \pi}{3}$
已知数列 $\left\{a_n\right\}$ 满足:$a_1=2, a_{n+1}=a_1+2 a_2+3 a_3+\cdots+n a_n$ ,令 $b_n=\frac{n+3}{a_{n+1}+a_{n+2}+a_{n+3}}$ ,数列 $\left\{b_n\right\}$ 的前 $n$项和 $S_n$ ,则 $S_{2025}=$
$\text{A.}$ $\frac{1}{8}-\frac{1}{2029!}$
$\text{B.}$ $\frac{1}{6}-\frac{1}{2028!}$
$\text{C.}$ $\frac{1}{4}-\frac{1}{2027!}$
$\text{D.}$ $\frac{1}{2}-\frac{1}{2026!}$
多选题 (共 3 题 ),每题有多个选项正确
2025年2月在黑龙江举行的第九届亚洲冬季运动会再次使冰雪经济成为关注热点.已知 2018-2024年中国冰雪运动核心市场规模(单位:亿元)依次为:454.3,487.5,445.2,594.9,713.9,833.1,1083.0.对于这 7 个数据,则
$\text{A.}$ 该组数据的极差是 628.7
$\text{B.}$ 该组数据的中位数是 594.9
$\text{C.}$ 该组数据的 $40 \%$ 分位数是 445.2
$\text{D.}$ 该组数据的平均数大于 630
若双曲线 $C$ 的两条渐近线的方程为 $y= \pm x$ ,则
$\text{A.}$ $C$ 的离心率为 $\sqrt{2}$
$\text{B.}$ $C$ 的焦点在 $x$ 轴上
$\text{C.}$ 若 $C$ 上的点到两渐近线距离之和的最小值为 4 ,则 $C$ 的实轴长为 $4 \sqrt{2}$
$\text{D.}$ 若双曲线 $y=\frac{8}{x}$ 绕原点沿逆时针方向旋转 $\frac{\pi}{4}$ 后恰好得到 $C$ ,则 $C$ 的方程为 $\frac{x^2}{16}-\frac{y^2}{16}=1$
已知定义在 $R$ 上的函数 $f(x)$ 满足:$\forall x_1, x_2 \in R , f\left(x_1 x_2\right)=f\left(x_1\right) f\left(x_2\right)-f\left(x_1\right)-f\left(x_2\right)+2$ ,且 $f(1) \neq 1$ ,则
$\text{A.}$ $f(1)=2$
$\text{B.}$ $f(x)$ 可能是偶函数
$\text{C.}$ $f(x)$ 的图象不可能关于点 $(0,1)$ 对称
$\text{D.}$ 若 $\forall x \in(1,+\infty), f(x)>2$ ,则 $f(x)$ 在 $(0,+\infty)$ 上单调递增
填空题 (共 3 题 ),请把答案直接填写在答题纸上
$\left(x+y^2-\frac{1}{y}\right)^9$ 的展开式中 $x^3 y^3$ 的系数为
已知点 $A, B, C, D$ 都在半径为 3 的球面上,且 $\triangle B C D$ 是边长为 $2 \sqrt{3}$ 的正三角形,则三棱锥 $A-B C D$体积的最大值为
若函数 $f(x)=\sin x-3|\sin x|$ 在 $\left[\frac{\pi}{2}, \alpha\right]$ 上的值域是 $[-2,0]$ ,则 $\alpha$ 的取值范围为 $\qquad$ ; $\sin ^2 \frac{\alpha}{4}$ $+\cos ^4 \frac{\alpha}{4}$ 的取值范围为
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
记 $\triangle A B C$ 的内角 $A, B, C$ 所对的边分别为 $a, b, c, a \sin A=3 b \sin C$ .
(1)求 $A$ 的最大值;
(2)若 $b \neq c$ ,且 $A=2 B$ ,求 $\cos C$ .
近年来我国在线音视频用户保持连续增长,李明绘制出 $2017 — 2024$ 年的年份代码 $x(x=1,2,3,4,5$ , $6,7,8)$ 与在线音视频用户数 $y$(单位:百万)的散点图,并求出 $y$ 关于 $x$ 的经验回归方程为 $\hat{y}=55.99 x$ $+333.42$.
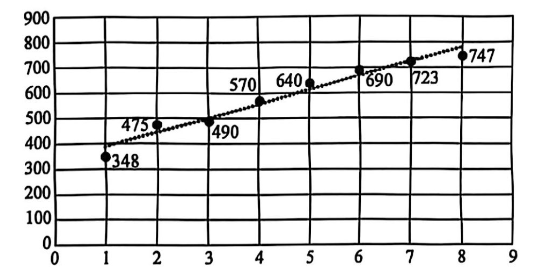
(1)求样本相关系数 $r$(精确到小数点后第二位,采用四舍五人法),判断经验回归方程是否有价值?
(2)从2017-2024年我国在线音视频用户数中随机抽取 3 个数据,记最小的数据为 $X$ ,求 $X$ 的分布列.
如图,在三棱锥 $A-B C D$ 中,$A B=B D=2, B C=C D=\sqrt{2}, A B \perp B D$ ,点 $E$ 为 $A D$ 的中点.
(1)求证:$B D \perp C E$ ;
(2)若平面 $A B D \perp$ 平面 $B C D$ ,求直线 $A C$ 与平面 $B C E$ 所成角的正弦值.
已知椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 及抛物线 $D: y^2=2 p x(p>0)$ 都经过点 $A\left(\frac{2}{3}, \frac{2 \sqrt{6}}{3}\right)$ ,且 $C$ 的右焦点与 $D$ 的焦点 $F$ 重合.
(1)求 $C$ 与 $D$ 的方程;
(2)过点 $E(2 p, 0)$ 作直线与 $C$ 交于 $P, Q$ 两点,与 $D$ 交于 $G, H$ 两点,过点 $F$ 作直线 $P Q$ 的平行线与 $C$交于 $M, N$ 两点.
( 1 )已知 $O$ 为原点,证明:$O G \perp O H$ ;
(II)判断是否存在常数 $k$ ,使得 $\overrightarrow{E P} \cdot \overrightarrow{E Q}+k \overrightarrow{F M} \cdot \overrightarrow{F N}=0$ ,并证明你的结论.
已知函数 $f(x), g(x)$ ,若 $\exists x_1, x_2, \cdots, x_k\left(k \in N ^*\right)$ ,使得 $f\left(x_i\right)=g\left(x_i\right)(i=1,2, \cdots, k)$ ,且 $f^{\prime}\left(x_i\right)=$ $g^{\prime}\left(x_i\right)$ ,则称 $f(x)$ 与 $g(x)$ 是"$k-A$ 类和谐函数";若 $\exists x_1, x_2, \cdots, x_k\left(k \in N ^*\right)$ ,使得 $f\left(x_i\right)=g\left(x_i\right)$ $(i=1,2, \cdots, k)$ ,且 $f^{\prime}\left(x_i\right) \neq g^{\prime}\left(x_i\right)$ ,则称 $f(x)$ 与 $g(x)$ 是"$k-B$ 类和谐函数".
(1)若 $f(x)=a \ln x$ 与 $g(x)=x^2$ 是" $1-A$ 类和谐函数",求 $y=f(x)$ 与 $y=g(x)$ 的图象在公共点处的切线方程;
(2)若 $f(x)=x^3+a x^2+1$ 与 $g(x)=x^3+x+\frac{3}{4} a$ 是"$k-A$ 类和谐函数",求 $k$ 与 $a$ 的值;
(3)求证:$f(x)=\sin x$ 与 $g(x)=\ln x$ 是" $1-B$ 类和谐函数".