已知函数 $f(x)=\sin (\omega x+\varphi)(\omega>0,|\varphi| < \pi)$ 的部分图象如图所示,则
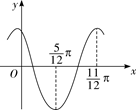
A
$\mathrm{f}(\mathrm{x})$ 的最小正周期为 $\pi$
B
$\varphi=\frac{\pi}{3}$
C
$\mathrm{f}(\mathrm{x})$ 的图象关于点 $\left(-\frac{4 \pi}{3}, 0\right)$ 中心对称
D
将 $\mathrm{f}(\mathrm{x})$ 图象上所有点的横坐标伸长为原来的 2 倍(纵坐标不变),得到函数 $\mathrm{g}(\mathrm{x})$ 的图象,则 $\mathrm{g}(\mathrm{x})$ 在区间 $\left[\pi, \frac{7 \pi}{4}\right]$ 上单调递增
E
F