单选题 (共 8 题 ),每题只有一个选项正确
复数 $z=\frac{2+4 \mathrm{i}}{\mathrm{i}}$ 在复平面内对应的点位于
$\text{A.}$ 第一象限
$\text{B.}$ 第二象限
$\text{C.}$ 第三象限
$\text{D.}$ 第四象限
设 $\mathrm{A}(0,-3), \mathrm{B}(0,3)$ 是平面内两个定点,动点 P 满足 $\|\mathrm{PA}|-| \mathrm{PB}\|=4$ ,则 $P$ 点的轨迹方程是
$\text{A.}$ $\frac{x^2}{4}-\frac{y^2}{5}=1$
$\text{B.}$ $\frac{y^2}{4}-\frac{x^2}{5}=1$
$\text{C.}$ $\frac{x^2}{5}-\frac{y^2}{4}=1$
$\text{D.}$ $\frac{y^2}{5}-\frac{x^2}{4}=1$
已知 $\mathrm{m}, \mathrm{n}$ 是两条不同的直线,$\alpha, \beta$ 是两个不同的平面,则
$\text{A.}$ 若 $m / / \alpha, n / / \alpha$ ,则 $m / / n$
$\text{B.}$ 若 $m / / \alpha, m \perp n$ ,则 $n \perp \alpha$
$\text{C.}$ 若 $\alpha / / \beta, \mathrm{m} \perp \alpha, \mathrm{n} / / \beta$ ,则 $\mathrm{m} \perp \mathrm{n}$
$\text{D.}$ 若 $\mathrm{m} / / \mathrm{n}, \mathrm{n} \perp \alpha$ ,则 $\mathrm{m} / / \alpha$
已知 $\boldsymbol{a}, \boldsymbol{b}$ 是夹角为 $120^{\circ}$ 的两个单位向量,则向量 $\boldsymbol{a}-3 \boldsymbol{b}$ 在向量 $\boldsymbol{a}$ 上的投影向量为
$\text{A.}$ $\frac{5}{2} a$
$\text{B.}$ $-\frac{1}{2} a$
$\text{C.}$ $-2 a$
$\text{D.}$ $4 \boldsymbol{a}$
圆 $\mathrm{C}_1: \mathrm{x}^2+\mathrm{y}^2-2 \mathrm{x}-4 \mathrm{y}+4=0$ 与圆 $\mathrm{C}_2:(\mathrm{x}-1)^2+(\mathrm{y}+2)^2=9$ 的位置关系为
$\text{A.}$ 内切
$\text{B.}$ 相交
$\text{C.}$ 外切
$\text{D.}$ 外离
已知实数 $\mathrm{x}, \mathrm{y}$ 满足 $\mathrm{y}=\frac{1}{5} \mathrm{x}-\frac{3}{5}$ ,且 $\mathrm{x} \in[-2,-1) \cup(-1,3]$ ,则 $\frac{\mathrm{y}-2}{\mathrm{x}+1}$ 的取值范围为
$\text{A.}$ $\left(-\infty,-\frac{1}{2}\right] \cup[3,+\infty)$
$\text{B.}$ $\left[-\frac{1}{2}, 3\right]$
$\text{C.}$ $(-\infty,-1] \cup[3,+\infty)$
$\text{D.}$ $[-1,3]$
已知点 $M(4,11)$ ,直线 $1_1: x+m y-3 m+4=0$ 与直线 $1_2: m x-y-2 m-5 =0$ 交于点 P ,则 $|\mathrm{PM}|$ 的值可以为
$\text{A.}$ 7
$\text{B.}$ 6
$\text{C.}$ 8
$\text{D.}$ 19
已知椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的左、右焦点分别为 $F_1, F_2, O$ 为坐标原点.若椭圆 C 上的点 M 满足 $|\mathrm{OM}|=\left|\mathrm{MF}_1\right|,\left|\mathrm{F}_1 \mathrm{~F}_2\right|=\left|\mathrm{MF}_2\right|$ ,则椭圆 C 的离心率为
$\text{A.}$ $2-\sqrt{2}$
$\text{B.}$ $\sqrt{3}-\sqrt{2}$
$\text{C.}$ $2-\sqrt{3}$
$\text{D.}$ $\sqrt{3}-1$
多选题 (共 3 题 ),每题有多个选项正确
已知点 $\mathrm{A}(2,3), \mathrm{B}(4,-5)$ 到直线 1 的距离相等,且 1 过点 $\mathrm{P}(1,2)$ ,则 1的方程可能是
$\text{A.}$ $x+4 y-6=0$
$\text{B.}$ $4 x+y-6=0$
$\text{C.}$ $2 x+3 y-7=0$
$\text{D.}$ $3 x+2 y-7=0$
已知函数 $f(x)=\sin (\omega x+\varphi)(\omega>0,|\varphi| < \pi)$ 的部分图象如图所示,则
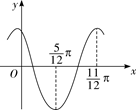
$\text{A.}$ $\mathrm{f}(\mathrm{x})$ 的最小正周期为 $\pi$
$\text{B.}$ $\varphi=\frac{\pi}{3}$
$\text{C.}$ $\mathrm{f}(\mathrm{x})$ 的图象关于点 $\left(-\frac{4 \pi}{3}, 0\right)$ 中心对称
$\text{D.}$ 将 $\mathrm{f}(\mathrm{x})$ 图象上所有点的横坐标伸长为原来的 2 倍(纵坐标不变),得到函数 $\mathrm{g}(\mathrm{x})$ 的图象,则 $\mathrm{g}(\mathrm{x})$ 在区间 $\left[\pi, \frac{7 \pi}{4}\right]$ 上单调递增
在正方体 $\mathrm{ABCDA}_1 \mathrm{~B}_1 \mathrm{C}_1 \mathrm{D}_1$ 中,点 P 为线段 $\mathrm{A}_1 \mathrm{C}$ 上的动点,则下列结论正确的是
$\text{A.}$ $\overrightarrow{\mathrm{A}_1 \mathrm{P}} \cdot \overrightarrow{\mathrm{AD}}_1=0$
$\text{B.}$ 平面 $\mathrm{DD}_1 \mathrm{C}_1 \mathrm{C}$ 与平面 $\mathrm{A}_1 \mathrm{D}_1 \mathrm{P}$ 所成角的正弦值是 $\frac{1}{2}$
$\text{C.}$ 当 $\overrightarrow{\mathrm{A}_1 \mathrm{P}}=\frac{1}{3} \overrightarrow{\mathrm{~A}_1 \mathrm{C}}$ 时, $\overrightarrow{\mathrm{D}_1 \mathrm{P}} \cdot \overrightarrow{\mathrm{AP}}$ 的值最小
$\text{D.}$ 若平面 ABCD 上的动点 M 满足 $\angle \mathrm{MD}_1 \mathrm{C}=\frac{\pi}{6}$ ,则点 M 的轨迹是椭圆
填空题 (共 3 题 ),请把答案直接填写在答题纸上
若直线 $y=x$ 与圆 $x^2+y^2-2 y=0$ 交于 $A, B$ 两点,则 $|A B|=$
在正四棱台 $\mathrm{ABCD} \mathrm{A}_1 \mathrm{~B}_1 \mathrm{C}_1 \mathrm{D}_1$ 中, $\mathrm{AB}=2, \mathrm{~A}_1 \mathrm{~B}_1=1, \mathrm{AA}_1=\sqrt{2}$ ,则该棱台的体积为
四位同学玩"石头剪刀布"的游戏.规则如下:四名同学同时参与,每人独立选择出"石头""剪刀"或"布"中的一种手势.若所有人出的手势完全相同(如全为石头),或三种手势都同时出现,则视为平局.否则,按照"石头胜剪刀,剪刀胜布,布胜石头"的规则判定胜负.已知每位同学出每种手势的概率均相等,则一次挑战中出现平局的概率为
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
在 $\triangle \mathrm{ABC}$ 中, $\mathrm{A}, \mathrm{B}, \mathrm{C}$ 所对的边分别为 $\mathrm{a}, \mathrm{b}, \mathrm{c}$ ,已知 $(2 \mathrm{c}-\mathrm{a}) \cos \mathrm{B}=\mathrm{b} \cos \mathrm{A}$ .
(1)求角 B 的大小;
(2)若 $\triangle \mathrm{ABC}$ 的面积为 $8 \sqrt{3}$ 且 $\mathrm{b}=6$ ,求 $\triangle \mathrm{ABC}$ 的周长.
甲、乙两人参加某高校的入学面试,入学面试有 3 道难度相当的题目,甲答对每道题目的概率都是 $\frac{2}{3}$ ,乙答对每道题目的概率都是 $\frac{1}{2}$ ,对抽到的不同题目能否答对是独立的,且甲、乙两人答题互不影响.
(1)求甲、乙两人共答对 5 道题目的概率;
(2)若每位面试者共有三次机会,一旦某次答对抽到的题目,则面试通过,否则就一直抽题到第 3 次为止,求甲、乙两人只有一人通过面试的概率.
已知椭圆 $\mathrm{C}: \frac{\mathrm{x}^2}{\mathrm{a}^2}+\frac{\mathrm{y}^2}{\mathrm{~b}^2}=1(\mathrm{a}>\mathrm{b}>0)$ 的长轴长为 4 ,且点 $(1, \mathrm{e})$ 在椭圆 C 上,其中 e 是椭圆 C 的离心率.
(1)求椭圆 C 的方程;
(2)若斜率为 $\frac{1}{2}$ 的直线 1 与椭圆 $C$ 交于 $M, N$ 两点,且点 $M$ 在第一象限,点 $A$ , B 分别为椭圆 C 的右顶点和上顶点,求四边形 AMBN 面积 S 的最大值.
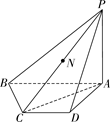
如图,在四棱锥 PABCD 中, $\mathrm{PA} \perp$ 平面 $\mathrm{ABCD}, \mathrm{BC} \perp \mathrm{AC}, \mathrm{AB} / / \mathrm{DC}$ .
(1)证明:平面 $P B C \perp$ 平面 $P A C$ ;
(2)若 $\mathrm{BC}=2, \mathrm{CD}=3, \mathrm{PA}=\mathrm{AB}=4, \mathrm{P}, \mathrm{A}, \mathrm{B}, \mathrm{C}$ 在同一个球面上,球心为 o.
(i)求 DO 与平面 PBC 所成角的正弦值;
(ii) N 为 PC 的中点,线段 PD 上是否存在点 H ,使得 $\mathrm{H}, \mathrm{A}, \mathrm{O}, \mathrm{N}$ 四点共面?若存在,求出点 H 的位置;若不存在,说明理由.
设函数 $f(x)=\sin ^{2 k} x+\cos ^{2 k} x, k \in N^*$ .
(1)求证:$f\left(\frac{\pi}{4}+x\right)=f\left(\frac{\pi}{4}-x\right)$ ;
(2)分别求 $k=2$ 和 $k=3$ 时函数 $f(x)$ 的最小值;
(3)求函数 $f(x)$ 的最小值(用 $k$ 表示).
参考公式:当 $n \in N^*$ 且 $n \geq 2$ 时,$a^n-b^n=(a-b)\left(a^{n^{-1}}+a^{n^{-2}} b+\ldots+a b^{n^{-2}}+b^{n^{-1}}\right)$ .