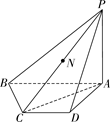
如图，在四棱锥 PABCD 中， $\mathrm{PA} \perp$ 平面 $\mathrm{ABCD}, \mathrm{BC} \perp \mathrm{AC}, \mathrm{AB} / / \mathrm{DC}$ ．
（1）证明：平面 $P B C \perp$ 平面 $P A C$ ；
（2）若 $\mathrm{BC}=2, \mathrm{CD}=3, \mathrm{PA}=\mathrm{AB}=4, \mathrm{P}, \mathrm{A}, \mathrm{B}, \mathrm{C}$ 在同一个球面上，球心为 o．
（i）求 DO 与平面 PBC 所成角的正弦值；
（ii） N 为 PC 的中点，线段 PD 上是否存在点 H ，使得 $\mathrm{H}, \mathrm{A}, \mathrm{O}, \mathrm{N}$ 四点共面？若存在，求出点 H 的位置；若不存在，说明理由．
$\text{A.}$
$\text{B.}$
$\text{C.}$
$\text{D.}$
$\text{E.}$
$\text{F.}$