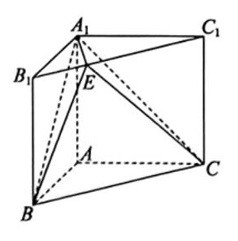
如图所示,在直三棱柱 $\mathrm{ABC}-\mathrm{A}_1 \mathrm{~B}_1 \mathrm{C}_1$ 中, $\mathrm{AB} \perp \underline{\mathrm{AC}}, \mathrm{AB}=\mathrm{AC}=\mathrm{CC}_1=1$ , E 是线段 $\mathrm{B}_1 \mathrm{C}_1$ 上的动点(不与点 $\mathrm{B}_1, \mathrm{C}_1$ 重合),且满足 $\overrightarrow{B_1 E}=\lambda \overrightarrow{B_1 C_1}$ ,实数 $\lambda \in(0,1)$ .
(1)当 $\lambda=\frac{1}{2}$ 时,证明: $\mathrm{A} 1 \mathrm{E} \perp$ 平面 EBC ;
(2)当 $\lambda=\frac{1}{3}$ 时,求二面角 $E-A_1 B-B_1$ 的余弦值;
(3)求四面体 $\mathrm{EA}_1 \mathrm{BC}$ 的外接球半径的取值范围.