单选题 (共 3 题 ),每题只有一个选项正确
设 $F_1(x), F_2(x)$ 是随机变量的分布函数,$f_1(x), f_2(x)$ 是相应的概率密度,则 $(\quad)$ .
$\text{A.}$ $F_1(x)+F_2(x)$ 是分布函数
$\text{B.}$ $F_1(x) \cdot F_2(x)$ 是分布函数
$\text{C.}$ $f_1(x)+f_2(x)$ 是概率密度
$\text{D.}$ $f_1(x) \cdot f_2(x)$ 是概率密度
通过某交叉路口的汽车流可以看作服从泊松分布.已知在 1 分钟内有汽车通过的概率为 0.7 ,则 1 分钟内最多有 1 辆汽车通过的概率为( )。
$\text{A.}$ $0.7(1-\ln 0.7)$
$\text{B.}$ $0.3(1-\ln 0.7)$
$\text{C.}$ $0.3(1-\ln 0.3)$
$\text{D.}$ $0.7(1-\ln 0.3)$
设随机变量 $X$ 服从正态分布 $N(0,1)$ ,对给定的 $\alpha(0 < \alpha < 1)$ ,数 $u_\alpha$ 满足 $P\left\{X>u_\alpha\right\}=\alpha$ ,若 $P\{|X| < x\}=\alpha$ ,则 $x$ 等于( ).
$\text{A.}$ $u_{\frac{\alpha}{2}}$
$\text{B.}$ $u_{1-\frac{\alpha}{2}}$
$\text{C.}$ $u_{\frac{1-\alpha}{2}}$
$\text{D.}$ $u_{1-\alpha}$
填空题 (共 2 题 ),请把答案直接填写在答题纸上
已知 $X$ 的分布函数为 $F(x)$ ,概率密度为 $f(x)$ .当 $x \leqslant 0$ 时,$f(x)$ 连续,且 $f(x)=F(x)$ ,若 $F(0)=1$ ,则 $f(x)=$ $\qquad$
已知 $X$ 为随机变量,$Y=X^2+X+1$ ,已知 $X$ 的概率分布为 $P\{X=-1\}=P\{X=0\}=P\{X=1\}=\frac{1}{3}$ ,则 $Y$ 的分布函数 $F_Y(y)=$ $\qquad$ .
解答题 (共 12 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设随机变量 $X$ 的分布函数为
$$
F(x)= \begin{cases}a+b e^{-x}, & x>0, \\ 0, & x \leqslant 0 .\end{cases}
$$
已知随机变量 $X$ 的概率分布为
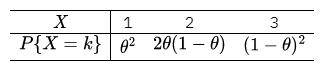
且 $P\{X \geqslant 2\}=\frac{3}{4}$ ,求未知参数 $\theta$ 及 $X$ 的分布函数 $F(x)$ .
设随机变量 $X$ 的概率密度为 $f(x)=\left\{\begin{array}{ll}2^{-x} \ln 2, & x>0, \\ 0, & \text { 其他.}\end{array}\right.$ 对 $X$ 进行独立重复的观测,直到第 2个大于 3 的观测值出现时停止,记 $Y$ 为观测次数.求 $Y$ 的概率分布.
某元件的工作寿命 $X$(小时)服从参数为 $\lambda(\lambda>0)$ 的指数分布.
(1)求该元件正常工作 $t$ 小时的概率;
(2)已知该元件已正常工作 10 小时,求在此基础上再工作 10 小时的概率 $(\lambda=0.01)$ .
设 $X \sim N\left(2, \sigma^2\right)$ ,且 $P\{2 < X < 4\}=0.3$ ,则 $P\{X < 0\}=$ $\qquad$ .
设随机变量 $X$ 和 $Y$ 同分布,$X$ 的概率密度为
$$
f(x)= \begin{cases}\frac{3}{8} x^2, & 0 < x < 2, \\ 0, & \text { 其他. }\end{cases}
$$
已知事件 $A=\{X>a\}$ 和 $B=\{Y>a\}$ 独立,且 $P(A \cup B)=\frac{3}{4}$ ,则常数 $a=$ $\qquad$ .
20 个产品中有 5 个不合格品,若从中随机取出 8 个,求其中不合格品数 $X$ 的概率分布.
已知离散型随机变量 $X$ 的正概率点为 $-1,0,2$ ,它们各自的概率互不相等且成等差数列.
(1)求 $X$ 的分布律;
(2)求 $X$ 的分布函数;
(3)求 $P\{|X| \leqslant 1 \mid X \geqslant 0\}$ .
随机变量 $X$ 的概率密度为
$$
f(x)= \begin{cases}x, & 0 \leqslant x < 1, \\ 2-x, & 1 \leqslant x < 2, \\ 0, & \text { 其他. }\end{cases}
$$
求 $X$ 的分布函数 $F(x)$ .
设随机变量 $X$ 的概率密度为 $f_X(x)=\frac{k}{1+x^2}(x \in R )$ .求:
(1)常数 $k$ ;
(2)随机变量 $Y=1-\sqrt[3]{X}$ 的概率密度 $f_Y(y)$ .
设随机变量 $X$ 的概率密度为 $f(x)=\frac{ e ^x}{\left(1+ e ^x\right)^2},-\infty < x < +\infty$ ,令 $Y= e ^X$ .
(1)求 $X$ 的分布函数;
(2)求 $Y$ 的概率密度.
设随机变量 $X \sim U(-1,2)$ ,求 $Y=|X|$ 的概率密度.