单选题 (共 5 题 ),每题只有一个选项正确
已知函数 $f(x)$ 满足:对任意 $x_1, x_2 \in[a, b]$ ,都有 $\frac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}>0$ ,且 $f(a) \cdot(b) < 0$ 。在用二分法寻找零点的过程中,依次确定了零点所在区间为 $[a, b],\left[a, \frac{a+b}{2}\right],\left[a+1, \frac{b}{3}\right]$ ,又 $f\left(\frac{a+2 b-4}{3}\right)=0$ ,则函数 $f(x)$ 的零点为
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $\frac{1}{3}$
$\text{C.}$ $\frac{1}{4}$
$\text{D.}$ $\frac{1}{5}$
若函数 $f(x)=x^3+x^2-2 x-2$ 的一个正数零点附近的函数值用二分法计算,其参考数据如下:
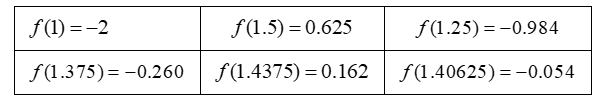
那么方程 $x^3+x^2-2 x-2=0$ 的一个近似根(精确度 0.05 )可以( ${ }^{\circ}$()
$\text{A.}$ 1.25
$\text{B.}$ 1.39
$\text{C.}$ 1.41
$\text{D.}$ 1.5
已知函数 $f(x)$ 的一个零点 $x_0 \in(2,4)$ ,用二分法求精确度为 0.01 的 $x_0$ 的近似值时,判断各区间中点的函数值的符号最多需要的次数为
$\text{A.}$ 6
$\text{B.}$ 7
$\text{C.}$ 8
$\text{D.}$ 9
函数 $f(x)=4^x+2 x-2$ 的零点与 $g(x)$ 的零点之差的绝对值不超过 $\frac{1}{4}$ ,则 $g(x)$ 的解析式可能是
$\text{A.}$ $g(x)=4 x-1$
$\text{B.}$ $g(x)=(x-1)^2$
$\text{C.}$ $g(x)= e ^x-1$
$\text{D.}$ $g(x)=\ln \left(x-\frac{1}{2}\right)$
已知图像连续不断的函数 $f(x)$ 在区间 $(a, b)(b-a=0.1)$ 上有唯一零点,如果用"二分法"求这个零点(精确度 0.0001 )的近似值,那么将区间 $(a, b)$ 等分的次数至少是
$\text{A.}$ 4
$\text{B.}$ 6
$\text{C.}$ 7
$\text{D.}$ 10