解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知函数 $f(x)=A \sin (\omega x+\varphi)(A>0, \omega>0,0 < \varphi < \pi)$ 的部分图像如图所示.
(I)求 $f(x)$ 的解析式;
(II)若 $f(x)$ 在区间 $[\pi, m)(m>\pi)$ 上存在最小值,求实数 $m$ 的取值范围.
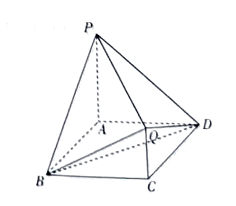
如图,在几何体 $A B C D P Q$ 中,$P A \perp$ 平面 $A B C D, Q C / / P A$ ,且 $Q C=\frac{1}{2} P A$ ,四边形 $A B C D$ 为菱形,$P A=A D=2, \angle B A D=120^{\circ}$ .
( I )求证:$B D \perp P Q$ ;
(II)求平面 $B P Q$ 与平面 $D P Q$ 夹角的余弦值.
在直角坐标系 $x O y$ 中,已知拖物线 $y^2=8 x$ 上两动点 $A, B$ 满足 $O A \perp O B$ .
( I )证明:直线 $A B$ 过定点;
(II)设直线 $A B$ 过定点 $P$ ,以 $O P$ 为直径作圆 $E$ ,过点 $(2,0)$ 且斜率为 $k(k \neq 0)$ 的直线 $l$ 与 $E$交于 $C, D$ 两点,将圆 $E$ 沿 $x$ 轴折起,使平而 $C O x \perp$ 平面 $D O x$ ,求折起后 $C D$ 的长度的取值范围。
( I )证明:$k C _n^k=n C _{n-1}^{k-1}$ ,其中 $n, k \in N ^*$ ,且 $2 \leqslant k \leqslant n$ .
(II)证明:若 $X$ 服从二项分布 $B(n, p)$ ,则 $E(X)=n p$ .
(III)甲,乙两人进行乒乓球比赛,每局甲放的概率为 $p\left(\frac{1}{2} < p < 1\right)$ ,乙噺的概率为 $q=$ $1-p$ .双方约定比满 $(2 n-1)$ 局,赢的局数多的人获胜.设甲获胜的概率为 $P_n$ ,证明 $\left\{P_n\right\}$ 是递增数列,并说明该结论的实际含义.
已知函数 $f(x)=\frac{ e ^x-b}{a x}$ 的图象在点 $(1, f(1))$ 处的切线方程为 $x-y+ e -2=0$ .
(I)求 $a, b$ 的值.
(II)若正项数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$ ,且 $a_{n+1}=\ln f\left(a_n\right), a_1=3$ ,证明:
( i )$a_{n+1} < a_n$ ;
( ii )$S_n \geqslant \frac{9}{2}\left(1-\frac{1}{3^n}\right)$ .