一、单选题 （共 19 题，每小题 5 分，共 50 分，每题只有一个选项正确）
已知函数 $f(x)=\left\{\begin{array}{l}-x^2-2 a x-a, x < 0 \\ e^x+\ln (x+1), x \geq 0\end{array}\right.$ 在 $R$ 上单调递增, 则 $a$ 的取值范围是
$\text{A.}$ $(-\infty, 0]$
$\text{B.}$ $[-1,0]$
$\text{C.}$ $[-1,1]$
$\text{D.}$ $[0,+\infty)$
已知函数的定义域为 $R, f(x)>f(x-1)+f(x-2)$ 且 $x < 3$ 时 $f(x)=x$, 则下列结论中一定正确的是
$\text{A.}$ $f(10)>100$
$\text{B.}$ $f(20)>1000$
$\text{C.}$ $f(10) < 1000$
$\text{D.}$ $f(20) < 10000$
已知命题 $p: \forall x \in \mathbf{R},|x+1|>1$; 命题 $q: \exists x>0, x^3=x$. 则
$\text{A.}$ $p$ 和 $q$ 都是真命题
$\text{B.}$ $\neg p$ 和 $q$ 都是真命题
$\text{C.}$ $p$ 和 $\neg q$ 都是真命题
$\text{D.}$ $\neg p$ 和 $\neg q$ 都是真命题
设函数 $f(x)=(x+a) \ln (x+b)$, 若 $f(x) \geqslant 0$, 则 $a^2+b^2$ 的最小值为
$\text{A.}$ $\frac{1}{8}$
$\text{B.}$ $\frac{1}{4}$
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ $1$
函数 $f(x)=-x^2+\left(e^x-e^{-x}\right) \sin x$ 的区间 $[-2.8,2.8]$ 的图像大致为
$\text{A.}$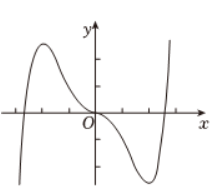 
$\text{B.}$ 
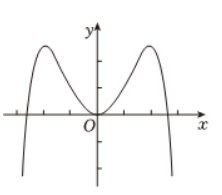$\text{C.}$ 
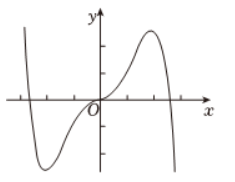$\text{D.}$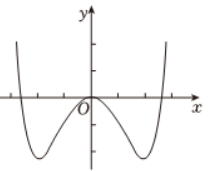 
设 $a \log _3 4=2$ ，则 $4^{-a}=$
$\text{A.}$ $\frac{1}{16}$
$\text{B.}$ $\frac{1}{9}$
$\text{C.}$ $\frac{1}{8}$
$\text{D.}$ $\frac{1}{6}$
已知奇函数 $f(x)$ 的定义域为 $\mathbf{R}$, 对任意的 $x$ 满足 $f(-x)=f(x+2)$, 且 $f(x)$ 在区间 $(-1,0)$ 上单调递增, 若 $a=\log _4 3, b=\log _\pi 2, c=\frac{1}{4} \log _{\sqrt{2}} 512 \sqrt{2}$, 则 $f(a), f(b), f(c)$ 的大小关系为
$\text{A.}$ $f(c)>f(a)>f(b)$
$\text{B.}$ $f(c)>f(b)>f(a)$
$\text{C.}$ $f(a)>f(b)>f(c)$
$\text{D.}$ $f(a)>f(c)>f(b)$
方程 $2^{\log _3 x}=\frac{1}{4}$ 的解是
$\text{A.}$ $x=\frac{1}{9}$
$\text{B.}$ $x=\frac{\sqrt{3}}{3}$
$\text{C.}$ $x=\sqrt{3}$
$\text{D.}$ ${x}=9$
如果奇函数 $f(x)$ 在区间 $[3,7]$ 上是增函数且最小值为 5 , 那么 $f(x)$ 在区间 $[-7$, $-3]$ 上是
$\text{A.}$ 增函数且最小值为一 5
$\text{B.}$ 增函数且最大值为 -5
$\text{C.}$ 减函数且最小值为 -5
$\text{D.}$ 减函数且最大值为 -5
$\frac{\log _8 9}{\log _2 3}$ 的值是
$\text{A.}$ $\frac{2}{3}$
$\text{B.}$ 1
$\text{C.}$ $\frac{3}{2}$
$\text{D.}$ 2
如果函数 ${f}({x})={x}^2+{bx}+{c}$ 对任意实数 t 都有 ${f}(2+{t})={f}(2-{t})$ ，那么
$\text{A.}$ ${f}(2) < {f}(1) < {f}(4)$
$\text{B.}$ ${f}(1) < {f}(2) < {f}(4)$
$\text{C.}$ ${f}(2) < {f}(4) < {f}(1)$
$\text{D.}$ ${f}(4) < {f}(2) < {f}(1)$
$y=x^{\frac{3}{5}}$ 在 $[-1,1]$ 上是
$\text{A.}$ 增函数且是奇函数
$\text{B.}$ 增函数且是偶函数
$\text{C.}$ 减函数且是奇函数
$\text{D.}$ 减函数且是偶函数
若 $a 、 b$ 是任意实数, 且 $a>b$, 则
$\text{A.}$ $a^2>b^2$
$\text{B.}$ $\frac{{b}}{{a}} < 1$
$\text{C.}$ $\lg (a-b)>0$
$\text{D.}$ $\left(\frac{1}{2}\right)^a < \left(\frac{1}{2}\right)^b$
某种细菌在培养过程中, 每 20 分钟分裂一次 (一个分裂为两个). 经过 3 小时, 这种细菌由 1 个可繁殖成
$\text{A.}$ 511 个
$\text{B.}$ 512 个
$\text{C.}$ 1023 个
$\text{D.}$ 1024 个
定义在 $(-\infty,+\infty)$ 上的任意函数 $f(x)$ 都可以表示成一个奇函数 $g(x)$ 和一个偶函数 $h(x)$ 之和, 如果 $f(x)=\lg \left(10^x+1\right), x \in(-\infty,+\infty)$, 那么
$\text{A.}$ $g(x)=x, \quad h(x)=\lg \left(10^x+10^{-x}+2\right)$
$\text{B.}$ $g(x)=\frac{1}{2}\left[\lg \left(10^x+1\right)+x\right], \quad h(x)=\frac{1}{2}\left[\lg \left(10^x+1\right)-x\right]$
$\text{C.}$ $g(x)=\frac{x}{2}, h(x)=\lg \left(10^x+1\right)-\frac{x}{2}$
$\text{D.}$ $g(x)=-\frac{x}{2}, h(x)=\lg \left(10^x+1\right)+\frac{x}{2}$
$f(x)$ 是 $(-\infty,+\infty)$ 上的奇函数, $f(x+2)=-f(x)$, 当 $0 \leq x \leq 1$ 时, $f(x)=x$, 则 $f(7.5)$ 等于
$\text{A.}$ 0.5
$\text{B.}$ -0.5
$\text{C.}$ 1.5
$\text{D.}$ -1.5
定义在区间 $(-\infty,+\infty)$ 的奇函数 $f(x)$ 为增函数；偶函数 $g(x)$ 在区间 $[0,+\infty)$ 的图像与 $f(x)$ 的图像重合, 设 $a>b>0$, 给出下列不等式:
(1) $f(b)-f(-a)>g(a)-g(-b) ;$
(2) $f(b)-f(-a) < g(a)-g(-b) ; \mid$
(3) $f(a)-f(-b)>g(b)-g(-a)$;
(4) $f(a)-f(-b) < g(b)-g(-a)$,
其中成立的是
$\text{A.}$ (1)与(4)
$\text{B.}$ (2)与(3)
$\text{C.}$ (1)与(3)
$\text{D.}$ (2)与(4)
函数 $f(x)=\frac{1}{x}(x \neq 0)$ 的反函数 $f^{-1}(x)=$
$\text{A.}$ $x(x \neq 0)$
$\text{B.}$ $\frac{1}{x}(x \neq 0)$
$\text{C.}$ $-x(x \neq 0)$
$\text{D.}$ $-\frac{1}{x}(x \neq 0)$
若函数 $y=f(x)$ 的反函数是 $y=g(x), f(a)=b, a b \neq 0$ ，则 $g(b)$ 等于
$\text{A.}$ $a$
$\text{B.}$ $a-1$
$\text{C.}$ $b$
$\text{D.}$ $b-1$
二、多选题 （共 3 题，每小题 5 分，共 20 分, 每题有多个选项符合要求，全部选对得 5 分，部分选对得 2 分，有选错得 0 分）
设函数 $f(x)=(x-1)^2(x-4)$, 则
$\text{A.}$ $x=3$ 是 $f(x)$ 的极小值点
$\text{B.}$ 当 $0 < x < 1$ 时, $f(x) < f\left(x^2\right)$
$\text{C.}$ 当 $1 < x < 2$ 时, $-4 < f(2 x-1) < 0$.
$\text{D.}$ 当 $-1 < x < 0$ 时, $f(2-x)>f(x)$
已知定义在区间 $[0, \pi]$ 上的函数 $f(x)=a x+\cos x$, 其中 $a \in \mathrm{R}$, 若函数 $f(x)$ 恰有两个极值点, 设其极大值、极小值分别记为 $m_1, m_2$. 则下列结论正确的是
$\text{A.}$ 函数 $f^{\prime}(x)$ 的图象关于直线 $x=\frac{\pi}{2}$ 对称
$\text{B.}$ 实数 $a$ 的取值范围为 $(0,1)$
$\text{C.}$ $m_1+m_2=a \pi$
$\text{D.}$ $m_1+m_2=a+a \pi$
已知函数 $f(x)$ 的定义域为 $\mathbf{R}, f(x+y)+2 x y=f(x)+f(y), f(1)=2$ ，则
$\text{A.}$ $f(0)=0$
$\text{B.}$ $f(-2)=-10$
$\text{C.}$ $y=f(x)+x^2$ 是奇函数
$\text{D.}$ $y=f(x)-x^2$ 是偶函数
三、填空题 （共 5 题, 每小题 5 分，共 20 分， 请把答案直接填写在答题纸上）
已知函数 $f(x)=a x^2+b x+c(b>a)$, 对于 $\left.\forall x \in R, f(x) \geq 0\right)$ 恒成立, 求 $\frac{b-a}{a+b+c}$ 的最大值是
已知 $f(m)=\left\{\begin{array}{l}m-1, m \text { 为奇数 } \\ \frac{m}{2}, m \text { 偶数 }\end{array}\right.$, 若 $a_0=\sum_{k=0}^{2024} 4^k, a_{n+1}=f\left(a^n\right)$ 满足 $a_k=0$ 的最小 $k$ 为
已知奇函数 $y=f(x)$ 在其定义域 $(-1,1)$ 上是减函数, 且 $f(1-a)+f\left(1-a^2\right) < 0$, 则 $a$ 的取值范围为
不等式 $6^{x^2+x-2} < 1$ 的解集是
方程 $\frac{1+3^{-x}}{1+3^x}=3$ 的解是
四、解答题 （ 共 13 题，满分 80 分，解答过程应写出必要的文字说明、证明过程或演算步骤 ）
已知函数 $y=f(x)(x \in R)$ 是偶函数. 当 $x \geq 0$ 时， $f(x)=x^2-4 x$.
(1) 求函数 $f(x)$ 在 $x \in R$ 上的解析式；
(2) 若函数 $f(x)$ 在区间 $[a, a+3]$ 上单调，求实数 $a$ 的取值范围；
(3)已知 $h(x)=|f(x)|-m$ ，试讨论 $h(x)$ 的零点个数，并求对应的 $m$ 的取值范围.
设函数 $y=f(x)$ 的定义域 $D \subseteq \mathrm{R}$, 若对任意 $x \in D$ ，均有 $f(-x) \neq-f(x)$ 成立，则称 $y=f(x)$ 为“无奇”函数.
(1)判断函数 ① $f(x)=x^2$ 和 ② $g(x)=\lg \frac{2-x}{1+x}$ 是否为“无奇”函数，说明理由；
(2) 若函数 $h(x)=3 x^3-2 x^2+x+a$ 是定义在 $[-1,2]$ 上的 “无奇”函数，求实数 $a$ 的取值范围；
(3) 若函数 $r(x)=\frac{1}{2^{x+1}+1}+m$ 是 “无奇”函数，求实数 $m$ 的取值范围.
$f(x)=1 g \frac{1+2^x+\cdots+(n-1)^x+n^x a}{n}$, 其中 $a$ 是实数, $n$ 是任意自然数且 $n \geqslant 2$.
(I) 如果 $f(x)$ 当 $x \in(-\infty, 1]$ 时有意义, 求 $a$ 的取值范围;
(II) 如果 $a \in(0,1]$, 证明 $2 \mathrm{f}(\mathrm{x}) < \mathrm{f}(2 \mathrm{x})$ 当 $\mathrm{x} \neq 0$ 时成立.
已知 $\mathrm{a}>0, \mathrm{a} \neq 1$, 解不等式 $\log a(4+3 x-x 2)-\log a(2 x-1)>\log a 2$.
根据函数单调性的定义, 证明函数 $f(x)=-x^3+1$ 在 $(-\infty,+\infty)$ 上是减函数.
已知 $n$ 为自然数, 实数 $a>1$, 解关于 $x$ 的不等式
$$
\log _2 x-\log _{a^2} x+12 \log _{a^3} x+\cdots+n(n-2)^{n-1} \log _{a^n} x>\frac{1-(-2)^n}{3} \log _a\left(x^2-a\right)
$$
设 $a>0, a \neq 1$, 解关于 $x$ 的不等式 $a^{x^4-2 x^2}>\left(\frac{1}{a}\right)^{a^2}$.
已知 $f(x)=\log _a \frac{1+x}{1-x}(a>0, a \neq 1)$.
(1) 求 $\mathrm{f}(\mathrm{x})$ 的定义域;
(2) 判断 f （x）的奇偶性并予以证明;
(3) 求使 $f(x)>0$ 的 $x$ 取值范围.
解方程 $\lg \left(x^2+4 x-26\right)-\lg (x-3)=1$.
某地现有耕地 10000 公顷，规划 10 年后粮食单产比现在增加 $22 \%$, 人均粮食占有量比现在提高 $10 \%$. 如果人口年增长率为 $1 \%$, 那么耕地平均每年至多只能减少多少公顷（精确到 1 公顷）?
（粮食单产 $=\frac{\text { 总产量 }}{\text { 耕地面积 }}$, 人均粮食占有量 $=\frac{\text { 总产量 }}{\text { 总人口数 }}$ )
已知 $a 、 b 、 c$ 是实数, 函数 $f(x)=a x^2+b x+c, g(x)=a x+b$, 当 $-1 \leqslant x \leqslant 1$ 时, $|f(x)| \leqslant 1$.
( I ) 证明: $|\mathrm{c}| \leqslant 1$ ；
(II) 证明: 当 $-1 \leqslant x \leqslant 1$ 时, $|g(x)| \leqslant 2$;
(III) 设 $a>0$, 当 $-1 \leqslant x \leqslant 1$ 时, $g(x)$ 的最大值为 2 , 求 $f(x)$.
设二次函数 $f(x)=a x^2+b x+c(a>0)$, 方程 $f(x)-x=0$ 的两个根 $x_1, x_2$ 满足 $0 < x_1 < x_2 < \frac{1}{a}$.
I. 当 $x \in\left(0, x_1\right)$ 时, 证明 $x < f(x) < x_1$;
II. 设函数 $f(x)$ 的图像关于直线 $x=x_0$ 对称, 证明 $x_0 < \frac{x_1}{2} 25$.