单选题 (共 6 题 ),每题只有一个选项正确
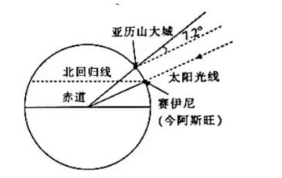
埃拉托斯特尼是古希腊亚历山大时期著名的地理学家, 他最出名的工作是计算了地球(大圆)的周长.如图, 在赛伊尼,夏至那天中午的太阳几乎正在天顶方向(这是从日光直射进该处一井内而得到证明的).同时在亚 历山大城(该处与赛伊尼几乎在同一子午线上), 其天顶方向与太阳光线的夹角测得为 $7.2^{\circ}$. 因太阳距离地球很 远, 故可把太阳光线看成是平行的.埃拉托斯特尼从商队那里知道两个城市间的实际距离大概是 5000 斯塔蒂亚, 按埃及的长度算, 1 斯塔蒂亚等于 $157.5$ 米, 则埃拉托斯特尼所测得地球的周长约为()
$\text{A.}$ 38680 千米
$\text{B.}$ 39375 千米
$\text{C.}$ 41200 千米
$\text{D.}$ 42192 千米
某几何体的三视图如右图所示, 则该几何体外接球的表面积为

$\text{A.}$ $200 \pi$
$\text{B.}$ $100 \pi$
$\text{C.}$ $\frac{125}{2} \pi$
$\text{D.}$ $50 \pi$
如图所示, 某三维形体的底面由曲线 $ y=\sqrt{\sec ^2 x+\tan x}\left(0 \leqslant x \leqslant \frac{\pi}{3}\right) $ 与 x 轴、 y 轴和 $ x=\frac{\pi}{3} $ 围成. 用垂直x轴的平面截该形体得到的节面均为正方形,则该形体的体积是

$\text{A.}$ $\frac{\sqrt{3}}{2}+\frac{\ln 2}{2}$
$\text{B.}$ $\frac{\sqrt{3}}{2}+\ln 2$
$\text{C.}$ $ \sqrt{3}+\frac{\ln 2}{2} $
$\text{D.}$ $\sqrt{3}+\ln 2$
$\text{E.}$ $\sqrt{3}+2 \ln 2$
坐标平面上的三个向量$ \vec{a}=(2,4), \quad \vec{b}=(2,8), \quad \vec{c}=(1,0)$
对于两个向量 $\vec{p}, \vec{q}$ 满足$
(\vec{p}-\vec{a}) \cdot(\vec{p}-\vec{b})=0, \quad \vec{q}=\frac{1}{2} \vec{ a}+t \vec{c}
$ , t是一个实数,求 $|\vec{p}-\vec{q}|$ 的最小值是多少?
$\text{A.}$ $\frac{3}{2}$
$\text{B.}$ 2
$\text{C.}$ $\frac{5}{2}$
$\text{D.}$ 3
$\text{E.}$ $\frac{7}{2}$
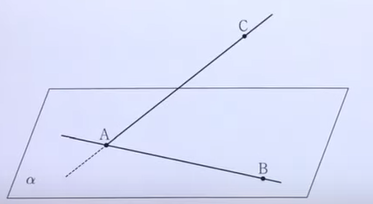
在坐标空间中有一个包含直线$\mathrm{AB}$的平面$\alpha$。 $\theta_1$ 是直线 $\mathrm{AB}$ 与直线 $\mathrm{AC}$ 所形成的锐角, $ \sin \theta_1=\frac{4}{5}$,直线$\mathrm{AC}$与平面$\alpha$形成的锐角的大小是 $\frac{\pi}{2}-\theta_1$ 。
如果$\theta_2$是平面$\mathrm{ABC}$与平面$\alpha$形成的锐角的大小,那么$\cos \theta_2$的值是多少?
$\text{A.}$ $\frac{\sqrt{7}}{4}$
$\text{B.}$ $\frac{\sqrt{7}}{5}$
$\text{C.}$ $\frac{\sqrt{7}}{6}$
$\text{D.}$ $\frac{\sqrt{7}}{7}$
$\text{E.}$ $\frac{\sqrt{7}}{8}$
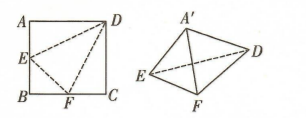
如图, 边长为 2 的正方形 $A B C D$ 中, 点 $E, F$ 分别是边 $A B, B C$ 的中 点, 将 $\triangle A E D, \triangle E B F, \triangle F C D$ 分别沿 $D E, E F, F D$ 折起, 使 $A, B, C$ 三点重合于点 $A^{\prime}$, 若四面体 $A^{\prime} E F D$ 的四个顶点在同一个球面上, 则 该球的半径为
$\text{A.}$ $\sqrt{2}$
$\text{B.}$ $\frac{\sqrt{6}}{2}$
$\text{C.}$ $\frac{\sqrt{11}}{2}$
$\text{D.}$ $\frac{\sqrt{5}}{2}$