单选题 (共 6 题 ),每题只有一个选项正确
设 $B$ 是椭圆 $C: \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a>b>0)$ 的上顶点, 若 $C$ 上的任意一点 $P$ 都满 足 $|\mathrm{PB}| \leq 2 \mathrm{~b}$, 则 $\mathrm{C}$ 的离心率的取值范围是 ( )
$\text{A.}$ $\left[\frac{\sqrt{2}}{2}, 1\right)$
$\text{B.}$ $\left[\frac{1}{2}, 1\right)$
$\text{C.}$ $\left(0, \frac{\sqrt{2}}{2}\right]$
$\text{D.}$ $\left(0, \frac{1}{2}\right]$
如图, 在平行六面体 (底面为平行四边形的四棱柱) $A B C D-A_1 B_1 C_1 D_1$ 中, $E$ 为 $B C$ 延长线上一点, $\overrightarrow{B C}=2 \overrightarrow{C E}$, 则 $\overrightarrow{D_1 E}$ 为
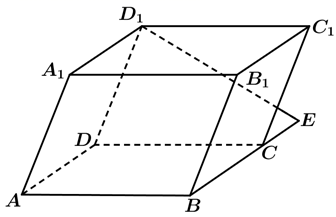
$\text{A.}$ $\overrightarrow{A B}+\overrightarrow{A D}+\overrightarrow{A A_1}$
$\text{B.}$ $\overrightarrow{A B}+\frac{1}{2} \overrightarrow{A D}-\overrightarrow{A A_1}$
$\text{C.}$ $\overrightarrow{A B}+\overrightarrow{A D}+\overrightarrow{A A_1}$
$\text{D.}$ $\overrightarrow{A B}+\frac{1}{3} \overrightarrow{A D}-\overrightarrow{A A_1}$
在二面角的棱上有两个点 $A 、 B$, 线段 $A C 、 B D$ 分别在这个二面角的两个面内, 并且都垂直于棱 $A B$, 若 $A B=1$, $A C=2, B D=3, C D=2 \sqrt{2}$, 则这个二面角的大小为
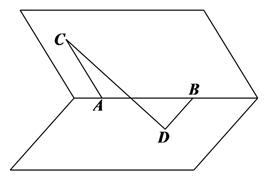
$\text{A.}$ $30^{\circ}$
$\text{B.}$ $45^{\circ}$
$\text{C.}$ $60^{\circ}$
$\text{D.}$ $90^{\circ}$
某玻璃制品厂需要生产一种如图 1 所示的玻璃杯, 该玻璃杯造型可以近似看成是一个 圆柱挖去一个圆台得到, 其近似模型的直观图如图 2 所示 (图中数据单位为 $\mathrm{cm}$ ), 则该 坡璃杯近似模型的体积 (单位: $\mathrm{cm}^3$ ) 为
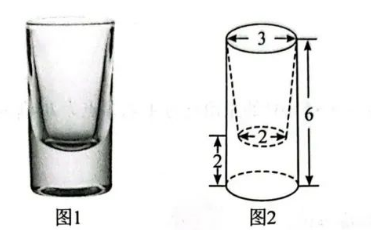
$\text{A.}$ $\frac{43 \pi}{6}$
$\text{B.}$ $\frac{47 \pi}{6}$
$\text{C.}$ $\frac{51 \pi}{6}$
$\text{D.}$ $\frac{55 \pi}{6}$
已知 $A, B, C, D$ 是半径为 $\sqrt{5}$ 的球体表面上的四点, $A B=2, \angle A C B=90^{\circ}, \angle A D B=30^{\circ}$, 则 平面 $C A B$ 与平面 $D A B$ 的夹角的余弦值为
$\text{A.}$ $\frac{\sqrt{6}-\sqrt{2}}{4}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $\frac{1}{3}$
$\text{D.}$ $\frac{\sqrt{3}}{3}$
已知圆锥的母线长为 1 , 其侧面展开图是一个圆心角为 $120^{\circ}$ 的扇形, 则该圆锥的轴截面面积为
$\text{A.}$ $\frac{2 \sqrt{5}}{9}$
$\text{B.}$ $\frac{2 \sqrt{2}}{9}$
$\text{C.}$ $\frac{\sqrt{5}}{9}$
$\text{D.}$ $\frac{\sqrt{2}}{9}$