单选题 (共 6 题 ),每题只有一个选项正确
已知 $f(x)=\frac{x e^x}{\mathrm{e}^{a x}-1}$ 是偶函数, 则 $a=$
$\text{A.}$ -2
$\text{B.}$ -1
$\text{C.}$ 1
$\text{D.}$ 2
设 $O$ 为平面坐标系的坐标原点, 在区域 $\left\{(x, y) \mid 1 \leqslant x^2+y^2 \leqslant 4\right\}$ 内随机取一点, 记该点为 $A$, 则直线 $O A$ 的 倾斜角不大于 $\frac{\pi}{4}$ 的概率为
$\text{A.}$
$\text{B.}$ $\frac{1}{6}$
$\text{C.}$ $\frac{1}{4}$
$\text{D.}$ $\frac{1}{2}$
甲乙两位同学从 6 种课外读物中各自选读 2 种, 则这两人选读的课外读物中恰有 1 种相同的选法共有
$\text{A.}$ 30 种
$\text{B.}$ 60 种
$\text{C.}$ 120 种
$\text{D.}$ 240 种
如图, 是某校随机抽取 50 名学生的身高与体重的 散点图, 则下列说法正确的是
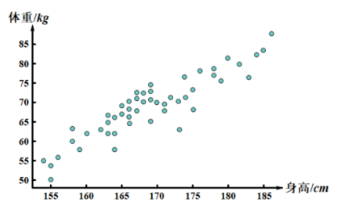
$\text{A.}$ 身高越高, 体重越重;
$\text{B.}$ 身高越高, 体重越轻;
$\text{C.}$ 身高与体重成正相关;
$\text{D.}$ 身高与体重成负相关.
设 $a>0$, 函数 $y=\sin x$ 在 $[a, 2 a]$ 上的最小值为 $s_a$, 在 $[2 a, 3 a]$ 上的最小值为 $t_a$, 当 $a$ 变化时, 则下列选 项不可能的是
$\text{A.}$ $s_a>0, t_a>0$
$\text{B.}$ $s_a < 0, t_a < 0$
$\text{C.}$ $s_a>0, t_a < 0$
$\text{D.}$ $s_a < 0, t_a>0$
$\forall x \in R$, 都有 $f\left(x^2+x+1\right)+3 f\left(x^2-3 x+3\right)=4 x^2-8 x+16$, 则
$\text{A.}$ $ f(2)=3$
$\text{B.}$ 存在 $p$, 使得 $f(p)=2023$
$\text{C.}$ $f(1)=0$
$\text{D.}$ 存在 $p$. 使得 $f(p)=-2023$