解答题 (共 2 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
小王早晨 7:30 从家出发上班,有 $A, B$ 两个出行方案供其选择,他统计了最近 100 天选择 $A, B$ 两个出行方案到达单位的时间,制成如下表格:
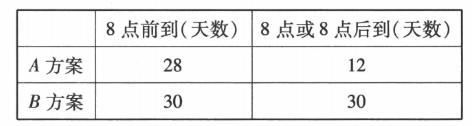
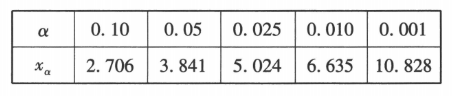
(1)根据小概率值 $\alpha=0.05$ 的独立性检验,判断 8点前到单位是否与出行方案选择有关。
(2)小王准备下周一选择 $A$ 方案上班,下周二至下周五选择 $B$ 方案上班,记小王下周一至下周五这 5 天中, 8 点前到单位的天数为随机变量 $X$ 。若用频率估计概率,求 $P(X=3)$ 。
附:$\chi^2=\frac{n(a d-b c)^2}{(a+b)(c+d)(a+c)(b+d)}$ ,其中 $n=a+$ $b+c+d$ 。
已知在 $\triangle A B C$ 中, $\sin ^2 A-\sin ^2 B=\sin ^2 C-$ $\sqrt{3} \sin B \sin C, 2 \cos B=\sin C$ 。
(1)判断 $\triangle A B C$ 的形状,并说明理由。
(2)点 $D$ 在 $A B$ 边上,且 $B D=2 A D$ 。若 $C D=2$ ,求 $\triangle A C D$ 的面积。