单选题 (共 6 题 ),每题只有一个选项正确
已知 $P_{1}\left(x_{1}, y_{1}\right), P_{2}\left(x_{2}, y_{2}\right)$ 是抛物线 $y=a x^{2}-2 a x$ 上的点, 下列命题正确的是 ( )
$\text{A.}$ 若 $\left|x_{1}-1\right|>\left|x_{2}-1\right|$, 则 $y_{1}>y_{2}$
$\text{B.}$ 若 $\left|x_{1}-1\right|>\left|x_{2}-1\right|$, 则 $y_{1} < y_{2}$
$\text{C.}$ 若 $\left|x_{1}-1\right|=\left|x_{2}-1\right|$, 则 $y_{1}=y_{2}$
$\text{D.}$ 若 $y_{1}=y_{2}$, 则 $x_{1}=x_{2}$
若 $\frac{a^2}{a^2-2}=\frac{1}{1-\sqrt{2}-\sqrt{3}}$, 则 $\left(\frac{1}{1-a}-\frac{1}{1+a}\right) \div\left(\frac{a}{a^2-1}+a\right)$ 的值是
$\text{A.}$ $\sqrt{2}-\sqrt{3}$
$\text{B.}$ $\sqrt{3}-\sqrt{2}$
$\text{C.}$ $-\sqrt{2}-\sqrt{3}$
$\text{D.}$ $\sqrt{2}+\sqrt{3}$
分解因式 $x^2+a x+b$ 时, Jagger看错了 $a$ 的值, 分解的结果是 $(x+6)(x-1), M e g$ 看错了 $b$ 的值, 分解的结果是 $(x$ $-2)(x+1)$, 那么正确的分解因式的结果是
$\text{A.}$ $(x+6)(x-2)$
$\text{B.}$ $(x+2)(x-3)$
$\text{C.}$ $(x+6)(x+1)$
$\text{D.}$ $(x-2)(x+3)$
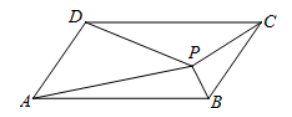
如图, 平行四边形 $A B C D$ 中, $P$ 是四边形内任意一点, $\triangle A B P, \triangle B C P, \triangle C D P, \triangle A D P$的面积分别为 $S_1, S_2, S_3, S_4$, 则一定成立的是
$\text{A.}$ $S_1+S_2=S_3+S_4$
$\text{B.}$ $S_1+S_2>S_3+S_4$
$\text{C.}$ $S_1+S_3=S_2+S_4$
$\text{D.}$ $S_1+S_2 < S_3+S_4$
对任意的整数 $x, y$, 定义 $x @ y=x+y-x y$, 则使得 $(x @ y) @ z+(y @ z) @ x+(z @ x) @ y$ $=0$ 的整数组 $(x, y, z)$ 的个数为
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
满足 $\left(x^2+x-1\right)^{x+2}=1$ 的整数 $x$ 的个数为
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4