单选题 (共 4 题 ),每题只有一个选项正确
设 $f(x)$ 在 $x=a$ 处可导,则
$$
\lim _{x \rightarrow 0} \frac{f(a+x)-f(a-x)}{x}=\text { ( ) }
$$
$\text{A.}$ $f^{\prime}(a)$
$\text{B.}$ $2 f^{\prime}(a)$
$\text{C.}$ 0
$\text{D.}$ $f^{\prime}(2 a)$
累次积分 $\int_0^{\frac{\pi}{2}} \mathrm{~d} \theta \int_0^{\cos \theta} f(r \cos \theta, r \sin \theta) r \mathrm{~d} r$
$\text{A.}$ $\int_0^1 \mathrm{~d} y \int_0^{\sqrt{y-y^2}} f(x, y) \mathrm{d} x$
$\text{B.}$ $\int_0^1 \mathrm{~d} y \int_0^{\sqrt{1-y^2}} f(x, y) \mathrm{d} x$
$\text{C.}$ $\int_0^1 \mathrm{~d} x \int_0^1 f(x, y) \mathrm{d} y$
$\text{D.}$ $\int_0^1 \mathrm{~d} x \int_0^{\sqrt{x-x^2}} f(x, y) \mathrm{d} y$
设 $F(x)=\int_x^{x+2 \pi} e^{\sin t} \sin t \mathrm{~d} t$ ,则 $F(x)$
$\text{A.}$ 为正常数
$\text{B.}$ 为负常数
$\text{C.}$ 恒为零
$\text{D.}$ 不为常数
如图,曲线方程为 $y=f(x)$ ,函数 $f(x)$ 在区间 $[0, a]$ 上有连续导数,则定积分 $\int_0^a x f^{\prime}(x) \mathrm{d} x$ 在几何上表示
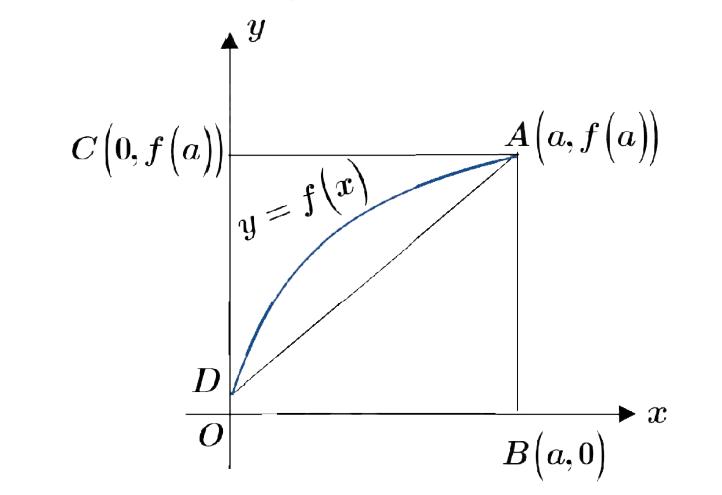
$\text{A.}$ 曲边梯形 $A B O D$ 的面积
$\text{B.}$ 梯形 $A B O D$ 的面积
$\text{C.}$ 曲边三角形 $A C D$ 面积
$\text{D.}$ 三角形 $A C D$ 面积
填空题 (共 2 题 ),请把答案直接填写在答题纸上
$\int f^{\prime}(x) \mathrm{d} x=$ $\qquad$ $\int_a^b f^{\prime}(2 x) d x=$
$\lim _{x \rightarrow+0}\left(\frac{1}{\sqrt{x}}\right)^{\tan x}=$