单选题 (共 18 题 ),每题只有一个选项正确
现有 5 幅不同的油画, 2 幅不同的国画, 7 幅不同的水彩画,从这些画中选一幅布置房间,则不同的选法共有
$\text{A.}$ 7 种
$\text{B.}$ 9 种
$\text{C.}$ 14 种
$\text{D.}$ 70 种
在中华传统文化里,建筑、器物、书法、诗歌、对联、绘画几乎无不讲究对称之美.如图所示的是清代诗人黄柏权的《茶壶回文诗》,其以连环诗的形式展现,20个字绕着茶壶成一圆环,无论顺着读还是逆着读,皆成佳作.数学与生活也有许多奇妙的联系,如2020年02月02日(20200202)被称为世界完全对称日(公历纪年日期中数字左右完全对称的日期).数学上把20200202这样的对称数叫回文数,如11,242,5225都是回文数,则用0,1,2,3,4,5这些数字构成的所有三位数的回文数中能被3整除的个数是

$\text{A.}$ 8
$\text{B.}$ 10
$\text{C.}$ 11
$\text{D.}$ 13
将编号 1,2,3,4的小球放入编号为 1,2, 3 的盒子中,要求不允许有空盒子,且球与盒子的号不能相同,则不同的放球方法有
$\text{A.}$ 16 种
$\text{B.}$ 12 种
$\text{C.}$ 9 种
$\text{D.}$ 6 种
如图,将钢琴上的 12 个键依次记为 $a_1, a_2, \ldots, a_{12}$ .设 $1 \leq i < j < k \leq 12$ .若 $k-j=3$ 且 $j- i=4$ ,则称 $a i, a j, a k$ 为原位大三和弦;若 $k-j=4$ 且 $j-i=3$ ,则称 $a i, a j, a k$ 为原位小三和弦.用这 12 个键可以构成的原位大三和弦与原位小三和弦的个数之和为
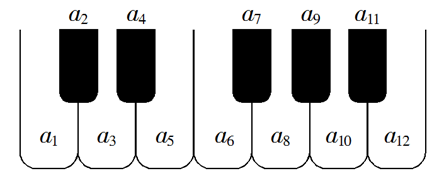
$\text{A.}$ 5
$\text{B.}$ 8
$\text{C.}$ 10
$\text{D.}$ 15
甲、乙分别从 4 门不同课程中选修 1 门,且 2 人选修的课程不同,则不同的选法有 种.
$\text{A.}$ 6
$\text{B.}$ 8
$\text{C.}$ 12
$\text{D.}$ 16
将 4 个不同的小球放入 3 个不同的盒子,其中有的盒子可能没有放球,则总的方法共有
$\text{A.}$ 81 种
$\text{B.}$ 64 种
$\text{C.}$ 36 种
$\text{D.}$ 18 种
如图,要让电路从A处到B处接通,不同的路径条数为
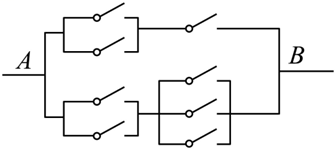
$\text{A.}$ 5
$\text{B.}$ 7
$\text{C.}$ 8
$\text{D.}$ 12
如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为
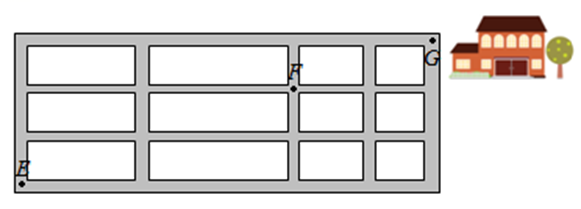
$\text{A.}$ 24
$\text{B.}$ 18
$\text{C.}$ 12
$\text{D.}$ 9
某人从上一层到二层需跨 10 级台阶,他一步可能跨 1 级台阶,称为一阶步,也可能跨 2 级台阶,称为二阶步,最多能跨 3 级台阶,称为三阶步,从一层上到二层他总共跨了 6 步,而且任何相邻两步均不同阶,则他从一层到二层可能的不同走法共有()种。
$\text{A.}$ 10
$\text{B.}$ 9
$\text{C.}$ 8
$\text{D.}$ 12
用四种颜色给下图的 6 个区域涂色,每个区域涂一种颜色,相邻区域不同色,若四种颜色全用上,则共有多少种不同的涂法
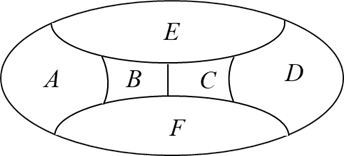
$\text{A.}$ 72
$\text{B.}$ 96
$\text{C.}$ 108
$\text{D.}$ 144
书桌上有 3 本不同的数学书和 4 本不同的语文书,从中任取数学书和语文书各 1 本,则不同的取法有
$\text{A.}$ 6 种
$\text{B.}$ 7 种
$\text{C.}$ 12 种
$\text{D.}$ 21 种
一个电路中含有(1)(2)两个零件,零件(1)含有 $A, B$ 两个元件,零件(2)含有 $C, D, E$ 三个元件,每个零件中有一个元件能正常工作则该零件就能正常工作,则该电路能正常工作的线路条数为
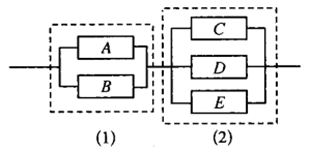
$\text{A.}$ 9
$\text{B.}$ 8
$\text{C.}$ 6
$\text{D.}$ 5
甲、乙、丙、丁四名交通志愿者申请在国庆期间到 三个路口协助交警值勤,他们申请值勤路口的意向如下表:

这4名志愿者的申请被批准,且值勤安排也符合他们的意向,若要求 三个路口都要有志愿者值勤,则不同的安排方法数有
$\text{A.}$ 14种
$\text{B.}$ 11种
$\text{C.}$ 8种
$\text{D.}$ 5种
为庆祝广益中学建校 130 周年,高二年级派出甲、乙、丙、丁、戊 5 名老师参加 " 130 周年办学成果展"活动,活动结束后 5 名老师排成一排合影留念,要求甲、乙两人不相邻且丙、丁两人必须相邻,则排法共有 种.
$\text{A.}$ 40
$\text{B.}$ 24
$\text{C.}$ 20
$\text{D.}$ 12
某市抽调 5 位老师分赴 3 所山区学校支教,要求每位老师只能去一所学校,每所学校至少安排一位老师.由于工作需要,甲、乙两位老师必须安排在不同的学校,则不同的分派方法的种数是
$\text{A.}$ 124
$\text{B.}$ 246
$\text{C.}$ 114
$\text{D.}$ 108
运输公司从 5 名男司机, 4 名女司机中选派出 3 名男司机, 2 名女司机,到 A , $B, C, D, E$ 这五个不同地区执行任务,要求 A 地只能派男司机,$E$ 地只能派女司机,则不同的方案种数是
$\text{A.}$ 360
$\text{B.}$ 720
$\text{C.}$ 1080
$\text{D.}$ 2160
第31届世界大学生夏季运动会于 6 月 26 日至 7 月 7 日在成都举办,现在从 6 男 4 女共 10 名青年志愿者中,选出 3 男 2 女共 5 名志愿者,安排到编号为 $1 、 2 、 3 、 4 、 5$ 的 5 个赛场,每个赛场只有一名志愿者,其中女志愿者甲不能安排在编号为 $1 、 2$ 的赛场,编号为 2 的赛场必须安排女志愿者,那么不同安排方案有
$\text{A.}$ 1440 种
$\text{B.}$ 2352 种
$\text{C.}$ 2880 种
$\text{D.}$ 3960 种
现有 5 名志愿者报名参加公益活动,在某一星期的星期六、星期日两天,每天从这 5 人中安排 2 人参加公益活动,则恰有 1 人在这两天都参加的不同安排方式共有
$\text{A.}$ 120
$\text{B.}$ 60
$\text{C.}$ 30
$\text{D.}$ 20
填空题 (共 10 题 ),请把答案直接填写在答题纸上
一个圆的圆周上均匀分布 6 个点,在这些点与圆心共 7 个点中,任取 3 个点,这 3 个点能构成不同的等边三角形个数为
已知集合 $A=\{2,4,6,8,10\}, B=\{1,3,5,7,9\}$ ,在 A 中任取一元素 $m$ ,在 $B$ 中任取一元素 $n$ ,组成数对 $(m, n)$ ,则其中 $m>n$ 的数对有多少个?
某学校举行校庆文艺晚会,已知节目单中共有七个节目,为了活跃现场气氛,主办方特地邀请了三位老校友演唱经典歌曲,并要将这三个不同节目添入节目单,而不改变原来的节目顺序,则不同的安排方式有 $\_\_\_\_$种。
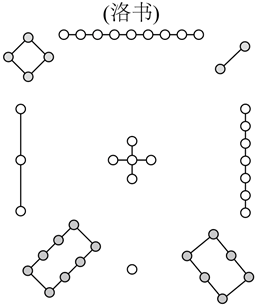
洛书,古称龟书,是阴阳五行术数之源,在古代传说中有神龟出于洛水,其甲壳上心有此图象如图,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,五方白圈皆阳数,四角黑点为阴数(图中白圈为阳数,黑点为阴数).现利用阴数和阳数构成一个四位数,规则如下:(从左往右数)第一位数是阳数,第二位数是阴数,第三位数和第四位数一阴一阳和为7,则这样的四位数有 () 个
2021年 12 月,南昌最美地铁 4 号线开通运营,甲、乙、丙、丁四位同学决定乘坐地铁去观洲、人民公园、新洪城大市场三个地方游览,每人只能去一个地方,人民公园一定要有人去,则不同游览方案的种数为 $\_\_\_\_$
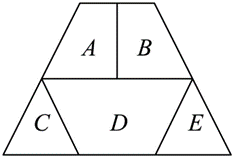
用红、黄、蓝、绿、橙五种不同颜色给如图所示的 5 块区域 A、B、C、D、 $E$ 涂色,要求同一区域用同一种颜色,有公共边的区域使用不同颜色,则共有涂色方法 $\_\_\_\_$
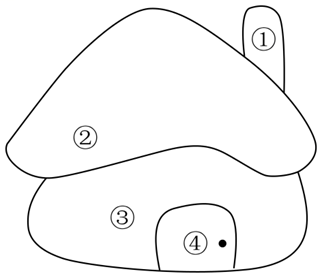
学习涂色能锻炼手眼协调能力,更能提高审美能力.现有四种不同的颜色:湖蓝色、米白色、橄榄绿、薄荷绿,欲给小房子中的四个区域涂色,要求相邻区域不涂同一颜色,且橄榄绿与薄荷绿也不涂在相邻的区域内,则共有 $\_\_\_\_$种不同的涂色方法.
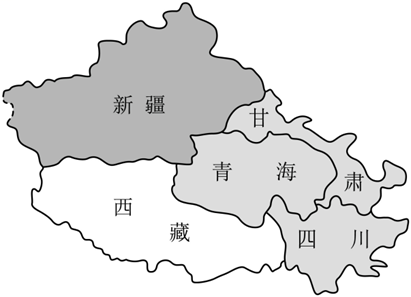
西部五省,有五种颜色供选择涂色,要求每省涂一色,相邻省不同色,有()种涂色方法.
有 5 张卡片,每张卡片的正反两面分别标有两个数字,且第 i 张卡片上的两个数字分别为 $2 i-2$ 和 $2 i-1(i=1,2,3,4,5)$ .用这五张卡片排成一排,一共可以组成 $\_\_\_\_$个不同的五位数(用数字作答)。
某学校开设了 4 门体育类选修课和 4 门艺术类选修课,学生需从这 8 门课中选修 2 门或 3 门课,并且每类选修课至少选修 1 门,则不同的选课方案共有 $\_\_\_\_$种(用数字作答)