单选题 (共 8 题 ),每题只有一个选项正确
设随机变量 $X$ 的分布函数为 $F(x)=\left\{\begin{array}{cl}0, & x < 0, \\ \frac{1}{2}, & 0 \leq x < 1, \\ 1-e^{-x}, & x \geq 1 .\end{array}\right.$ 则 $P\{X=1\}=$
$\text{A.}$ 0
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $\frac{1}{2}-e^{-1}$
$\text{D.}$ $1-e^{-1}$
设随机变量 $X$ 的概率分布为 $P\{X=k\}=A \lambda^k, k=1,2, \cdots$ ,且 $A>0$ ,则 $\lambda=()$ 。
$\text{A.}$ $A+1$
$\text{B.}$ $\frac{1}{A+1}$
$\text{C.}$ $\frac{1}{A-1}$
$\text{D.}$ 大于零的任意实数
做一系列独立试验,每次试验成功的概率均为 $p$ ,则在 3 次成功之前失败 4 次的概率为
$\text{A.}$ $12 p^4(1-p)^3$
$\text{B.}$ $12 p^3(1-p)^3$
$\text{C.}$ $15 p^3(1-p)^4$
$\text{D.}$ $15 p^4(1-p)^3$
下列函数可作为连续型随机变量 $X$ 的概率密度的是
$\text{A.}$ $f(x)=\left\{\begin{array}{l}2,-1 < x < 1, \\ 0, \quad \text { 其他.}\end{array}\right.$
$\text{B.}$ $f(x)=\left\{\begin{array}{lc}x^2, & -1 < x < 1, \\ 0, & \text { 其他.}\end{array}\right.$
$\text{C.}$ $f(x)=\left\{\begin{array}{lc}\frac{1}{2}, & -1 < x < 1, \\ 0, & \text { 其他.}\end{array}\right.$
$\text{D.}$ $f(x)=\left\{\begin{array}{l}x,-1 < x < 1, \\ 0, \quad \text { 其他.}\end{array}\right.$
设 $F_1(x), F_2(x)$ 为两个分布函数,相应的概率密度为 $f_1(x), f_2(x)$ 是连续函数,则必为概率密度的是( )。
$\text{A.}$ $f_1(x) f_2(x)$
$\text{B.}$ $2 f_2(x) F_1(x)$
$\text{C.}$ $f_1(x) F_2(x)$
$\text{D.}$ $f_1(x) F_2(x)+f_2(x) F_1(x)$
设随机变量 $X$ 服从正态分布,其概率密度 $f(x)$ 在 $x=1$ 处有驻点,且 $f(1)=1$ ,则 $X$ 服从正态分布( )。
$\text{A.}$ $N(0,1)$
$\text{B.}$ $N(1,1)$
$\text{C.}$ $N\left(1, \frac{1}{2 \pi}\right)$
$\text{D.}$ $N\left(1, \frac{1}{\sqrt{2 \pi}}\right)$
设随机变量 $X \sim N\left(\mu, \sigma^2\right)$ ,且满足 $P\{X < \sigma\}>P\{X>\sigma\}$ ,则 $\frac{\mu}{\sigma}$ 的值().
$\text{A.}$ 小于 1
$\text{B.}$ 等于 1
$\text{C.}$ 大于 1
$\text{D.}$ 不确定
设 $f_1(x)$ 为标准正态分布的概率密度,$f_2(x)$ 为 $[-1,3]$ 上的均匀分布,若 $f(x)=\left\{\begin{array}{lll}a f_1(x), & x \leq & 0 \\ b f_2(x), & x> & 0\end{array}(a>0, b \quad\right.$ ,则 $a, b$ 应满足( )。
$\text{A.}$ $2 a+3 b=4$
$\text{B.}$ $3 a+2 b=4$
$\text{C.}$ $a+b=1$
$\text{D.}$ $a+b=2$
填空题 (共 1 题 ),请把答案直接填写在答题纸上
若随机变量 $Y \sim E(1)$ ,则 $P\{Y \leq a+1 \mid Y>a\}=$
解答题 (共 13 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设陏机变量 $X$ 的分布函数为
$$
F(x)= \begin{cases}\frac{a x}{1+x}+b, & x>0 \\ 0, & x \leq 0\end{cases}
$$
求常数 $a, b$ 及概率 $P\{1 < X \leq 2\}$ .
设随机变量 $X$ 的分布律为
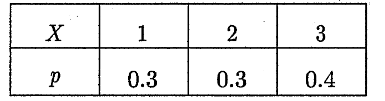
试求(1)$X$ 的分布函数 $F(x)$ ;(2)$P\{1 < X < 2.5\} 、 P\{X>1\}$ .
设随机变量 $X$ 的分布函数为 $F(x)=\left[\begin{array}{ll}0, & x < -1, \\ 0.4, & -1 \leq x < 1, \\ 0.8, & 1 \leq x < 3, \\ 1, & x \geq 3 .\end{array}\right.$ 试求 $X$ 的分布律.
设随机变量 $X \sim B(2, p)$ ,随机变量 $Y \sim B(3, p)$ 的二项分布,若 $P(X \geq 1)=\frac{5}{9}$ ,求 $P\{Y \geq 1\}$ .
设随机变量 $X$ 的分布律为 $P\{X=k\}=\frac{C}{k!}, k=0,1,2, \cdots$, 求概率 $P\{X>1\}$ .
设某批电子元件的正品率为 $\frac{4}{5}$ ,现对这批元件进行测试,只要测得一个正品就停止测试工作,则测试次数 $X$ 的分布律为
盒中有 12 只乒乓球,其中有 2 只是新的, 10 只是用过的,从盒中任取 3 只球,求取出的 3 只球中新球数 $X$ 的分布律
设连续型随机变量 $X$ 的分布函数为 $F(x)=\left\{\begin{array}{cc}0, & x < -a, \\ A+B \arcsin \frac{x}{a}, & -a \leq x < a \\ 1, & x \geq a .\end{array}\right.$其中 $a>0$ .(1)求常数 $A, B$ ;(2)求 $P\left\{-\frac{a}{2} \leq X \leq \frac{a}{2}\right\}$ .
设连续型随机变量 $X$ 的概率密度函数为 $f(x)=\left\{\begin{array}{lc}c x(1-x), 0 < x < 1 \\ 0, & \text { 其他 }\end{array}\right.$
(1)求常数 $c$ ;(2)求概率 $P\left(|X| \leq \frac{1}{2}\right)$ ;(3)求 $X$ 的分布函数 $F(x)$ .
设随机变量 $X$ 在区间 $\left[1,6\right.$ 上服从均匀分布,则方程 $x^2+X x+1=0$ 有实根的概率为
设随机变量 $X$ 的概率分布为
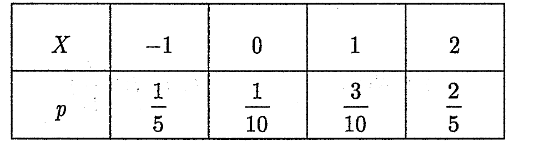
求(1)$Y=2 X$ 的分布律;(2)$Y=X^2$ 的分布律.
设连续型随机变量的概率密度为 $f(x)=\left\{\begin{array}{cc}2 x, & 0 < x < 1, \\ 0, & \text { 其他.}\end{array}\right.$ .
(1)求 $Y=-X+1$ 的密度函数;(2)求 $Y=X^2$ 的密度函数.
设随机变量 $X \sim E(1)$ ,求随机变量 $Y=e^X$ 的概率密度函数 $f_Y(y)$ .