单选题 (共 6 题 ),每题只有一个选项正确
已知 $P$ 是等边三角形 $A B C$ 所在平面内一点, 且 $A B=2 \sqrt{3}, B P=1$, 则 $\overrightarrow{A P} \cdot \overrightarrow{C P}$ 的最 小值是
$\text{A.}$ $1$
$\text{B.}$ $\sqrt{2}$
$\text{C.}$ $\sqrt{3}$
$\text{D.}$ $2$
已知单位向量 $\vec{a}$ 与向量 $\vec{b}=(0,2)$ 垂直, 若向量 $\vec{c}$ 满足 $|\vec{a}+\vec{b}+\vec{c}|=1$, 则 $|\vec{c}|$ 的取值范围 为
$\text{A.}$ $[1, \sqrt{5}-1]$
$\text{B.}$ $\left[\frac{\sqrt{3}-1}{2}, \frac{\sqrt{3}+1}{2}\right]$
$\text{C.}$ $[\sqrt{5}-1, \sqrt{5}+1]$
$\text{D.}$ $\left[\frac{\sqrt{3}+1}{2}, 3\right]$
已知向量 $\vec{a}, \vec{b}$ 满足 $\vec{a}=(\sqrt{3}, 1), \vec{a} \cdot \vec{b}=4$, 则 $|\vec{b}|$ 的最小值为
$\text{A.}$ 1
$\text{B.}$ $\sqrt{2}$
$\text{C.}$ $\sqrt{3}$
$\text{D.}$ 3
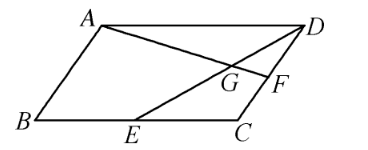
在平行四边形 $A B C D$ 中, $E, F$ 分别是 $B C, C D$ 的中点, $D E$ 交 $A F$ 点 $G$, 则 $\overrightarrow{A G}=$
$\text{A.}$ $\frac{2}{5} \overrightarrow{A B}-\frac{4}{5} \overrightarrow{B C}$
$\text{B.}$ $\frac{2}{5} \overrightarrow{A B}+\frac{4}{5} \overrightarrow{B C}$
$\text{C.}$ $-\frac{2}{5} \overrightarrow{A B}+\frac{4}{5} \overrightarrow{B C}$
$\text{D.}$ $-\frac{2}{5} \overrightarrow{A B}-\overrightarrow{B C}$
已知点 $O$ 为 $\triangle A B C$ 所在平面内的一点, 且 $\overrightarrow{O A}^2=\overrightarrow{O B}^2=\overrightarrow{O C}^2, \overrightarrow{O A} \cdot \overrightarrow{O B}=\overrightarrow{O B} \cdot \overrightarrow{O C}=\overrightarrow{O C}$. $\overrightarrow{O A}=-2$, 则 $\triangle A B C$ 的面积为
$\text{A.}$ $\sqrt{3}$
$\text{B.}$ $2 \sqrt{3}$
$\text{C.}$ $3 \sqrt{3}$
$\text{D.}$ $\frac{5 \sqrt{3}}{4}$
在 $\triangle A B C$ 中, $\overrightarrow{A B} \cdot \overrightarrow{A C}=9, \sin (A+C)=\cos A \sin C, S_{\triangle A B C}=6, P$ 为线段 $A B$ 上的动 点, 且 $\overrightarrow{C P}=x \cdot \frac{\overrightarrow{C A}}{|\overrightarrow{C A}|}+y \cdot \frac{\overrightarrow{C B}}{|\overrightarrow{C B}|}$, 则 $\frac{2}{x}+\frac{1}{y}$ 的最小值为
$\text{A.}$ $\frac{11}{6}+\frac{\sqrt{6}}{3}$
$\text{B.}$ $\frac{11}{6}$
$\text{C.}$ $\frac{11}{12}+\frac{\sqrt{6}}{3}$
$\text{D.}$ $\frac{11}{12}$