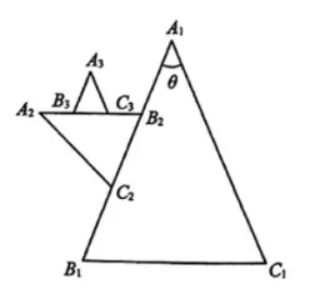
如图，已知给定线段 $B_1 C_1$ 长为 2 ，以 $B_1 C_1$ 为底边作顶角为 $\theta\left(0^{\circ} < \theta \leq 90^{\circ}\right)$ 的等腰三角形 $A_1 B_1 C_1$ ，取 $\triangle A_1 B_1 C_1$ 的腰 $A_1 B_1$ 的三等分点 $B_2, C_2\left(B_2\right.$ 靠近 $\left.A_1\right)$ ，以 $B_2 C_2$ 为底边向 $\triangle A_1 B_1 C_1$ 外部作顶角为 $\theta$ 的等腰三角形 $A_2 B_2 C_2 \cdots \cdots$ 依次类推，取 $\triangle A_{n-1} B_{n-1} C_{n-1}$ 的腰 $A_{n-1} B_{n-1}$ 的三等分点 $B_n, C_n\left(B_n\right.$ 靠近 $\left.A_{n-1}\right)$ ，以 $B_n C_n$ 为底边向 $\triangle A_{n-1} B_{n-1} C_{n-1}$ 外部作顶角为 $\theta$ 的等腰三角形 $A_n B_n C_n(n \geq 2)$ ，得到三角形列 $\left\{\triangle A_n B_n C_n\right\}$ ．
（1）用 $\theta$ 表示出 $\triangle A_2 B_2 C_2$ 的外接圆半径；
（2）当 $\theta=60^{\circ}$ 时，证明：$\left\{\triangle A_n B_n C_n\right\}$ 各顶点均在 $\triangle A_1 B_1 C_1$外接圆上或其内部；
（3）若 $\left\{\triangle A_n B_n C_n\right\}$ 各顶点均在 $\triangle A_1 B_1 C_1$ 外接圆上或其内部，求 $\cos \theta$ 的取值范围．

(深圳中学 2025 届高三二轮三阶测试)设函数 $f(x)=A \sin \frac{\pi x}{2}+g(x), x \in R ($ 其中常数 $A \in R , A>0)$ ，无穷数列 $\left\{a_n\right\}$ 满足：首项 $a_1>0, a_{n+1}=$ $f\left(a_n\right), n \in N^*$ ．
（1）若 $g(x)=B \sin ^2 \frac{\pi x}{8}, B \in R$ ，试判断函数 $y=f(x)$ 的奇偶性和最小正周期，并说明理由；
（2）若 $g(x)=x$ ，
（1）已知对任意的 $n \in N^*, a_{n+1}>a_n$ ，求证：当 $A < 4$ 时，数列 $\left\{a_n\right\}$ 不是等差数列；
（2）当 $A=8$ 时，数列 $\left\{a_n\right\}$ 是否可能为公比小于 0 的等比数列？若可能，求出所有公比的值；若不可能，请说明理由．

（长郡中学 2025 届高三考前适应性演）设 $a>b>0, m>0$ ，点 $A, ~ F$ 分别是椭圆 $\Gamma: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ 的上顶点与右焦点，且 $|A F|=2$ ，直线 $l: x$ $-m y-1=0$ 经过点 $F$ 与 $\Gamma$ 交于 $P, ~ Q$ 两点，$O$ 是坐标原点．
（1）求椭圆 $\Gamma$ 的方程；
（2）若 $m=\sqrt{3}$ ，点 $M$ 是 $x$ 轴上的一点，且 $\triangle M P Q$ 的面积为 $\frac{6}{13}$ ，求点 $M$ 的坐标；
（3）若点 $G$ 在直线 $x=5$ 上，向量 $\overrightarrow{P G}$ 在直线 $l$ 上的投影为向量 $\overrightarrow{P F}$ ，证明 $\angle P G Q < \frac{\pi}{4}$ ．