单选题 (共 6 题 ),每题只有一个选项正确
设随机变量 $X$ 的分布列为:
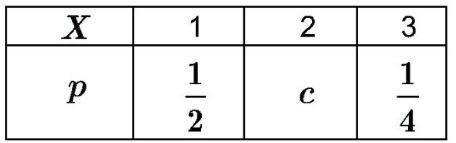
则常数 $c= $
$\text{A.}$ 0
$\text{B.}$ 1
$\text{C.}$ $\frac{1}{4}$
$\text{D.}$ $-\frac{1}{4}$
设 $X \sim N(0,1)$ ,又常数 $c$ 满足 $P\{X \geq c\}=P\{X < c\}$ ,则 $c=$
$\text{A.}$ 1
$\text{B.}$ 0
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ -1
下列结论中, ________ 不是随机变量 $X$ 与 $Y$ 不相关的充 要条件.
$\text{A.}$ $E(X Y)=E(X) E(Y)$
$\text{B.}$ $D(X+Y)=D X+D Y$
$\text{C.}$ $\operatorname{Cov}(X, Y)=0$
$\text{D.}$ $X$ 与 $Y$ 相互独立
设是二维离散型随机变量,则 $X$ 与 $Y$ 独立的充要条件是
$\text{A.}$ $E(X Y)=E X E y$
$\text{B.}$ $D(X+Y)=D X+D Y$
$\text{C.}$ $X$ 与 $Y$ 不相关
$\text{D.}$ 对 $(X, Y)$ 的任何可能取值 $\left(x_i, y_j\right), P_{i j}=P_{i \bullet} \cdot P_{\cdot j}$
设 $(X, Y)$ 联合密度为 $p(x, y)=\left\{\begin{array}{cc}4 x y, & 0 \leq x, y \leq 1 \\ 0, & \text { 其它 , }\end{array}\right.$ 若 $F(x, y)$ 为分布函数,则 $F(0.5,2)= $
$\text{A.}$ 0
$\text{B.}$ $\frac{1}{4}$
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ 1
设随机变量 $X \sim N(0,1)$, 以 $|X|$ 为半径作圆, 独立重复操作 10000 次, 所得各圆的面积和为 $S$, 则 $S$ 服从
$\text{A.}$ 正态分布.
$\text{B.}$ $t$ 分布.
$\text{C.}$ $\chi^2$ 分布.
$\text{D.}$ 三者都不对.