解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设 $f(x)$ 的二阶导函数连续, 且 $\lim _{x \rightarrow 0} \frac{f(x)+\cos x}{x^2}=1$, 求 $f(0), f^{\prime}(0), f^{\prime \prime}(0)$.
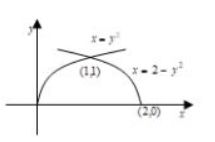
设曲线 $x=y^2(y>0), x=2-y^2(y>0)$ 及 $y=0$ 围成一平面图形 D.
(1) 求平面图形 D 的面积;
(2) 求平面图形 D 绕 $y$ 轴旋转一周而成的立体的体积
计算函数 $ y=\left(\frac{x}{1+x}\right)^x $ 的一阶导数
设函数 $f(x)$ 在 $(-\infty,+\infty)$ 上二阶可导, 函数 $g(x)=\left\{\begin{array}{cc}a x^2+b x+c & x>0 \\ f(x) & x \leq 0\end{array}\right.$, 试确定常数 $a, b, c$ 的值, 使得函数 $g(x)$ 在 $x=0$ 点二阶可导.
证明:当 $ x> 0 $ 时, $ 1+x \ln \left(x+\sqrt{1+x^2}\right)>\sqrt{1+x^2} $
设 $y=y(x)$ 满足 $x^2 y^{\prime}+y=x^2 \mathrm{e}^{\frac{1}{x}}(x \neq 0)$, 且 $y(1)=3 \mathrm{e}$.
(I) 求 $y=y(x)$ 的全部渐近线方程;
(II) 讨论曲线 $y=y(x)$ 与 $y=k(k>0)$ 不同交点的个数.