已知椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的左，右焦点分别为 $F_1, F_2$ ，下顶点为 $A$ ，直线 $A F_1$ 交 $C$ 于另一点 $B, \triangle A B F_2$ 的内切圆分别与 $B F_2, A F_1, A F_2$ 相切于点 $P, M, N$ ．若 $|B P|=\left|F_1 F_2\right|$ ，则 $C$ 的离心率为

新高考数学试卷增加了多项选择题，每小题有 $A , B , C , D$ 四个选项，有多个选项符合题目要求，由于正确选项有 4 个的概率极低，可视作 0 ，因此我们可以认为多项选择题至少有 2 个正确选项，至多有 3 个正确选项。多项选择题题目要求：＂在每小题给出的选项中，有多项符合题目要求。全部选对的得 6 分，部分选对的得部分分，有选错的得 0 分．＂其中＂部分选对的得部分分＂是指：若正确答案有 2 个选项，则只选 1 个选项且正确得 3 分；若正确答案有 3 个选项，则只选 1 个选项且正确得 2 分，只选 2 个选项且都正确得 4 分．
（1）已知某道多选题的正确答案是 AB ，一考生在解答该题时，完全没有思路，随机选择至少 1 个选项，至多 3 个选项，且每种选择是等可能的．请根据已知材料，分析该生可能的得分情况与所得分值的相应概率，并求该生得分的期望。
（2）已知某道多选题的正确答案是 2 个选项或是 3 个选项的概率相等，一考生只能判断出 A 选项是正确的，其他选项均不能判断正误，试列举出该生所有可能的符合实际的答题方案，并以各方案得分的期望作为判断依据，帮该考生选出恰当方案．

有三家公司都为毕业生小李提供了求职面试的机会，这三家公司分别记为 $A, B, C$ ，每家公司都可以提供很好，好和一般三种职位，每家公司将根据面试情况决定给予求职者何种职位或拒绝提供职位。规定供需双方在面试以后要立即决定提供或拒绝提供，接受或拒绝某种职位，且不容许毁约．咨询专家对小李的学业成绩和综合素质进行评估后认为他获得很好，好，一般职位的可能性分别为 $0.2,0.3,0.4$ ．三家公司的见习期工资数据如下表所示（单位：元）：

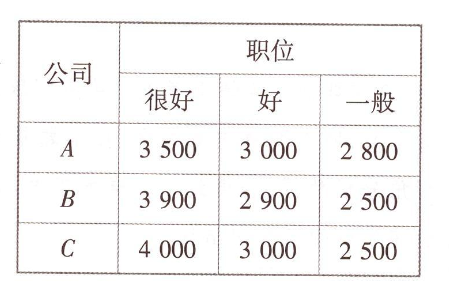
面试顺序有两种方案，方案一是小李自己决定面试顺序；方案二是按规定的 $A, B, C$ 顺序去面试。请你为小李选择一个合适的方案（若选择方案一，请写出面试顺序；若选择方案二，请写出具体的面试策略）．

定义：由椭圆的两个焦点和短轴的一个端点组成的三角形称为该椭圆的＂特征三角形＂。如果两个椭圆的＂特征三角形＂相似，则称这两个椭圆是＂相似椭圆＂，并将三角形的相似比称为椭圆的相似比．已知椭圆 $C_1: \frac{x^2}{4}+y^2=1$ ．
（1）椭圆 $C_2: \frac{x^2}{16}+\frac{y^2}{4}=1$ ，判断 $C_2$ 与 $C_1$ 是否相似．如果相似，求出 $C_2$ 与 $C_1$ 的相似比；如果不相似，请说明理由。
（2）写出与椭圆 $C_1$ 相似且短半轴长为 $b$ ，焦点在 $x$ 轴上的椭圆 $C_b$ 的标准方程（用含 $b$ 的式子表示）．若在椭圆 $C_b$ 上存在两点 $M, N$ 关于直线 $y=x+1$ 对称，求实数 $b$ 的取值范围．