单选题 (共 17 题 ),每题只有一个选项正确
如图,在矩形 $A B C D$ 中,分别以点 A 和 $C$ 为圆心,$A D$ 长为半径画弧,两弧有且仅有一个公共点.若 $A D=4$ ,则图中阴影部分的面积为
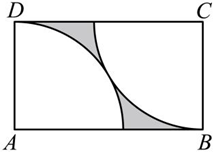
$\text{A.}$ $32-8 \pi$
$\text{B.}$ $16 \sqrt{3}-4 \pi$
$\text{C.}$ $32-4 \pi$
$\text{D.}$ $16 \sqrt{3}-8 \pi$
如图,$O$ 是坐标原点,菱形 $A B O C$ 的顶点 $B$ 在 $x$ 轴的负半轴上,顶点 $C$ 的坐标为 $(3,4)$ ,则顶点 A 的坐标为
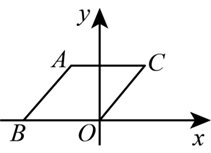
$\text{A.}$ $(-4,2)$
$\text{B.}$ $(-\sqrt{3}, 4)$
$\text{C.}$ $(-2,4)$
$\text{D.}$ $(-4, \sqrt{3})$
小美同学按如下步骤作四边形 $A B C D$ :(1)画 $\angle M A N$ ;(2)以点 A 为圆心, 1 个单位长为半径画弧,分别交 $A M$ , $A N$ 于点 $B, D$ ;(3)分别以点 $B, D$ 为圆心, 1 个单位长为半径画弧,两弧交于点 $C$ ;(4)连接 $B C, C D, B D$ .若 $\angle A=44^{\circ}$ ,则 $\angle C B D$ 的大小是
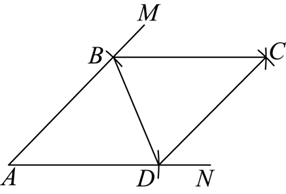
$\text{A.}$ $64^{\circ}$
$\text{B.}$ $66^{\circ}$
$\text{C.}$ $68^{\circ}$
$\text{D.}$ $70^{\circ}$
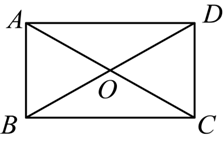
如图,在矩形 $A B C D$ 中,对角线 $A C$ 与 $B D$ 相交于点 $O$ ,则下列结论一定正确的是
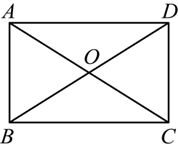
$\text{A.}$ $A B=A D$
$\text{B.}$ $A C \perp B D$
$\text{C.}$ $A C=B D$
$\text{D.}$ $\angle A C B=\angle A C D$
如图,四边形 $A B C D$ 是菱形,$C D=5, B D=8, A E \perp B C$ 于点 $E$ ,则 $A E$ 的长是
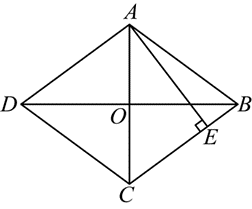
$\text{A.}$ $\frac{24}{5}$
$\text{B.}$ 6
$\text{C.}$ $\frac{48}{5}$
$\text{D.}$ 12
在平面直角坐标系中,我们把一个点的纵坐标与横坐标的比值称为该点的"特征值".如图,矩形 $A B C D$ 位于第一象限,其四条边分别与坐标轴平行,则该矩形四个顶点中"特征值"最小的是
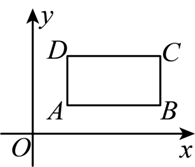
$\text{A.}$ 点 $A$
$\text{B.}$ 点 $B$
$\text{C.}$ 点 $C$
$\text{D.}$ 点 $D$
如图,在平面直角坐标系中,点 $A$ 的坐标为 $(-4,0)$ ,点 $C$ 的坐标为 $(0,2)$ .以 $O A, O C$ 为边作矩形 $O A B C$ ,若将矩形 $O A B C$ 绕点 $O$ 顺时针旋转 $90^{\circ}$ ,得到矩形 $O A^{\prime} B^{\prime} C^{\prime}$ ,则点 $B^{\prime}$ 的坐标为
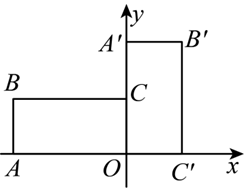
$\text{A.}$ $(-4,-2)$
$\text{B.}$ $(-4,2)$
$\text{C.}$ $(2,4)$
$\text{D.}$ $(4,2)$
如图,在矩形 $A B C D$ 中,对角线 $A C, B D$ 相交于点 $O, \angle A B D=60^{\circ}, A B=2$ ,则 $A C$ 的长为
$\text{A.}$ 6
$\text{B.}$ 5
$\text{C.}$ 4
$\text{D.}$ 3
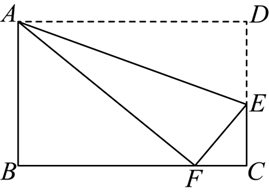
如图,在矩形 $A B C D$ 中,$A B=6, B C=8$ ,点 $E$ 在 $D C$ 上,把V $A D E$ 沿 $A E$ 折叠,点 $D$ 恰好落在 $B C$ 边上的点 $F$ 处,则 $\cos \angle C E F$ 的值为
$\text{A.}$ $\frac{\sqrt{7}}{4}$
$\text{B.}$ $\frac{\sqrt{7}}{3}$
$\text{C.}$ $\frac{3}{4}$
$\text{D.}$ $\frac{5}{4}$
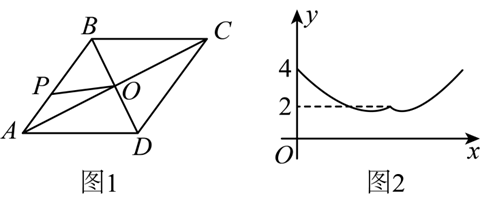
如图 1,动点 $P$ 从菱形 $A B C D$ 的点 $A$ 出发,沿边 $A B \rightarrow B C$ 匀速运动,运动到点 $C$ 时停止.设点 $P$ 的运动路程为 $x, P O$ 的长为 $y, y$ 与 $x$ 的函数图象如图 2 所示,当点 $P$ 运动到 $B C$ 中点时,$P O$ 的长为
$\text{A.}$ 2
$\text{B.}$ 3
$\text{C.}$ $\sqrt{5}$
$\text{D.}$ $2 \sqrt{2}$
如图 1,矩形 $A B C D$ 中,$B D$ 为其对角线,一动点 $P$ 从 $D$ 出发,沿着 $D \rightarrow B \rightarrow C$ 的路径行进,过点 $P$ 作 $P Q \perp C D$ ,垂足为 $Q$ .设点 $P$ 的运动路程为 $x, P Q-D Q$ 为 $y, y$ 与 $x$ 的函数图象如图 2 ,则 $A D$ 的长为
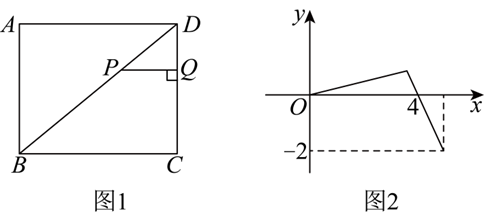
$\text{A.}$ $\frac{4 \sqrt{2}}{3}$
$\text{B.}$ $\frac{8}{3}$
$\text{C.}$ $\frac{7 \sqrt{3}}{4}$
$\text{D.}$ $\frac{11}{4}$
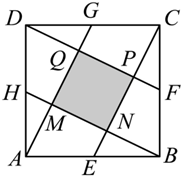
如图,边长为 5 的正方形 $A B C D, E, F, G, H$ 分别为各边中点,连接 $A G, B H, C E, D F$ ,交点分别为 $M, N, P, Q$ ,那么四边形 $M N P Q$ 的面积为
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 5
$\text{D.}$ 10
如图,边长为 2 的正方形 $A B C D$ 的对角线 $A C$ 与 $B D$ 相交于点 $O . E$ 是 $B C$ 边上一点,$F$ 是 $B D$ 上一点,连接 $D E, E F$ .若 $ D E F$ 与 $ D E C$ 关于直线 $D E$ 对称,则 $\triangle B E F$ 的周长是

$\text{A.}$ $2 \sqrt{2}$
$\text{B.}$ $2+\sqrt{2}$
$\text{C.}$ $4-2 \sqrt{2}$
$\text{D.}$ $\sqrt{2}$
四边形 $A B C D$ 为矩形,过 $A, ~ C$ 作对角线 $B D$ 的垂线,过 $B, ~ D$ 作对角线 $A C$ 的垂线,如果四个垂线拼成一个四边形,那这个四边形为
$\text{A.}$ 菱形
$\text{B.}$ 矩形
$\text{C.}$ 直角梯形
$\text{D.}$ 等腰梯形
宽与长的比是 $\frac{\sqrt{5}-1}{2}$ 的矩形叫黄金矩形,黄金矩形给我们以协调的美感,世界各国许多著名建筑为取得最佳的视觉效果,都采用了黄金矩形的设计.已知四边形 $A B C D$ 是黄金矩形。 $(A B < B C)$ ,点 $P$ 是边 $A D$ 上一点,则满足 $P B \perp P C$ 的点 $P$ 的个数为
$\text{A.}$ 3
$\text{B.}$ 2
$\text{C.}$ 1
$\text{D.}$ 0
如图,在边长为 6 的正方形 $A B C D$ 中,点 $E, F$ 分别是边 $A B, B C$ 上的动点,且满足 $A E=B F, A F$ 与 $D E$ 交于点 $O$ ,点 $M$ 是 $D F$ 的中点,$G$ 是边 $A B$ 上的点,$A G=2 G B$ ,则 $O M+\frac{1}{2} F G$ 的最小值是
$\text{A.}$ 4
$\text{B.}$ 5
$\text{C.}$ 8
$\text{D.}$ 10
如图,在边长为 4 的正方形 $A B C D$ 中,点 $E$ 是 $B C$ 上一点,点 $F$ 是 $C D$ 延长线上一点,连接 $A E, A F, A M$平分 $\angle E A F$ .交 $C D$ 于点 $M$ .若 $B E=D F=1$ ,则 $D M$ 的长度为
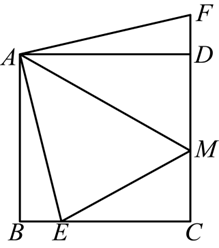
$\text{A.}$ 2
$\text{B.}$ $\sqrt{5}$
$\text{C.}$ $\sqrt{6}$
$\text{D.}$ $\frac{12}{5}$
填空题 (共 9 题 ),请把答案直接填写在答题纸上
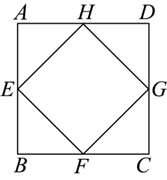
如图,正方形 $A B C D$ 的面积为 4 ,点 $E, F, G, H$ 分别为边 $A B, B C, C D, A D$ 的中点,则四边形 $E F G H$的面积为
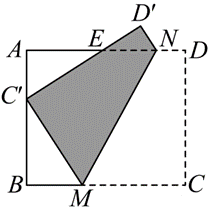
将一张矩形纸片(四边形 $A B C D$ )按如图所示的方式对折,使点 $C$ 落在 $A B$ 上的点 $C^{\prime}$ 处,折痕为 $M N$ ,点 $D$ 落在点 $D^{\prime}$ 处,$C^{\prime} D^{\prime}$ 交 $A D$ 于点 $E$ .若 $B M=3, B C^{\prime}=4, A C^{\prime}=3$ ,则 $D N=$
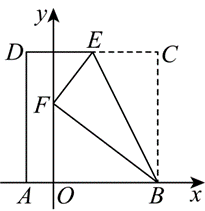
如图,在平面直角坐标系中,正方形 $A B C D$ 的边 $A B$ 在 $x$ 轴上,点 $A$ 的坐标为 $(-2,0)$ ,点 $E$ 在边 $C D$ 上.将 $\triangle B C E$ 沿 $B E$ 折叠,点 $C$ 落在点 $F$ 处.若点 $F$ 的坐标为 $(0,6)$ ,则点 $E$ 的坐标为
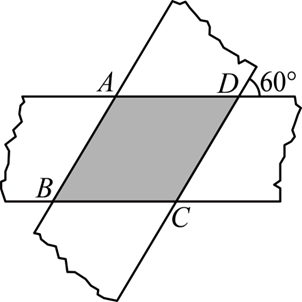
如图,两张宽度均为 3 cm 的纸条交叉叠放在一起,交叉形成的锐角为 $60^{\circ}$ ,则重合部分构成的四边形 $A B C D$的周长为 $\qquad$ cm
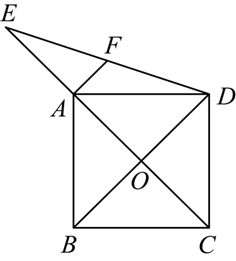
如图,正方形 $A B C D$ 的边长为 $3 \sqrt{2}$ ,对角线 $A C, B D$ 相交于点 $O$ ,点 $E$ 在 $C A$ 的延长线上,$O E=5$ ,连接 $D E$ .
(1)线段 $A E$ 的长为 $\qquad$ ;
(2)若 $F$ 为 $D E$ 的中点,则线段 $A F$ 的长为 $\qquad$ .
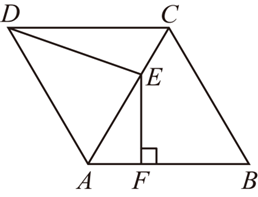
如图,在菱形 $A B C D$ 中,$\angle A B C=60^{\circ}, A B=6, A C$ 是一条对角线,$E$ 是 $A C$ 上一点,过点 $E$ 作 $E F \perp A B$ ,垂足为 $F$ ,连接 $D E$ .若 $C E=A F$ ,则 $D E$ 的长为
如图,菱形 $A B C D$ 的面积为 24 ,点 $E$ 是 $A B$ 的中点,点 $F$ 是 $B C$ 上的动点.若 $\triangle B E F$的面积为 4 ,则图中阴影部分的面积为

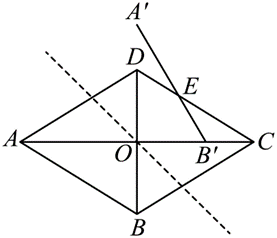
如图,在菱形 $A B C D$ 中,对角线 $A C, B D$ 相交于点 $O, \frac{A C}{B D}=\frac{5}{3}$ .线段 $A B$ 与 $A^{\prime} B^{\prime}$ 关于过点 $O$ 的直线 $l$ 对称,点 $B$ 的对应点 $B^{\prime}$ 在线段 $O C$ 上,$A^{\prime} B^{\prime}$ 交 $C D$ 于点 $E$ ,则 $\triangle B^{\prime} C E$ 与四边形 $O B^{\prime} E D$ 的面积比为 $\qquad$
在矩形 $A B C D$ 中,$A B=4 cm, B C=8 cm$ ,点 $E$ 在直线 $A D$ 上,且 $D E=2 cm$ ,则点 $E$ 到矩形对角线所在直线的距离是 $\qquad$ cm .