如图, 在菱形 $A B C D$ 中, $A B=6, \angle B=30^{\circ}$, 点 $E$ 是 $B C$ 边上的动点, 连接 $A E, D$ $E$, 过点 $A$ 作 $A F \perp D E$ 于点 $F$. 设 $D E=x, A F=y$, 则 $y$ 与 $x$ 之间的函数解析式为 (不考虑自变量 $x$的取值范围）

（ $2024 \cdot$ 长沙 ）为庆祝中国改革开放 46 周年，某中学举办了一场精彩纷呈的庆祝活动，现场参与者均为在校中学生，其中有一个活动项目是"选数字猜出生年份", 该活动项目主持人要求参与者从 $1,2,3,4,5,6,7,8,9$ 这九个数字中任取一个数字, 先乘以 10 ,再加上 4.6 ，将此时的运算结果再乘以 10 ，然后加上 1978 ，最后减去参与者的出生年份（注：出生年份是一个四位数，比如 2010 年对应的四位数是 2010 ），得到最终的运算结果。只要参与者报出最终的运算结果，主持人立马就知道参与者的出生年份。若某位参与者报出的最终的运算结果是 915 , 则这位参与者的出生年份是 .

计算: $\left(\frac{1}{4}\right)^{-1}+|-\sqrt{3}|-2 \cos 30^{\circ}-(\pi-6.8)^0$.

先化简, 再求值: $2 m-m(m-2)+(m+3)(m-3)$, 其中 $m=\frac{5}{2}$.

如图, 在Rt $\triangle A B C$ 中, $\angle A C B=90^{\circ}, A B=2 \sqrt{5}, A C=2$, 分别以点 $A, B$ 为圆心, 大于 $\frac{1}{2} A B$ 的长为半径画弧, 两弧分别交于点 $M$ 和 $N$, 作直线 $M N$ 分别交 $A B, B C$ 于点 $D, E$, 连接 $C D, A E$.
(1) 求 $C D$ 的长；
(2) 求 $\triangle A C E$ 的周长.

中国新能源产业异军突起。中国车企在政策引导和支持下, 瞄准纯电、混动和氢燃料等多元技术路线, 加大研发投入形成了领先的技术优势. 2023 年, 中国新能源汽车产销量均突破 900 万辆, 连续 9 年位居全球第一。在某次汽车展览会上, 工作人员随机抽取了部分参展人员进行了"我最喜欢的汽车类型"的调查活动（每人限选其中一种类型），并将数据整理后，绘制成下面有待完成的统计表、条形统计图和扇形统计图.

请根据以上信息, 解答下列问题:
( 1 ) 本次调查活动随机抽取了 $\qquad$人；表中 $a=$ $\qquad$ ,$b=$ $\qquad$ ; ?
（2）请补全条形统计图:
（3）请计算扇形统计图中"混动"类所在扇形的圆心角的度数；
（4）若此次汽车展览会的参展人员共有 4000 人, 请你估计喜欢新能源（纯电、混动、氢燃料）汽车的有多少人?

如图, 点 $C$ 在线段 $A D$ 上, $A B=A D, \angle B=\angle D, B C=D E$.
(1) 求证: $\triangle A B C \cong \triangle A D E$;
(2) 若 $\angle B A C=60^{\circ}$, 求 $\angle A C E$ 的度数.

刺绣是我国民间传统手工艺，湘绣作为中国四大刺绣之一，闻名中外，在巴黎奥运会倒计时 50 天之际，某国际旅游公司计划购买 $A 、 B$ 两种奥运主题的湘绣作品作为纪念品。已知购买 1 件 $A$ 种湘绣作品与 2 件 $B$ 种湘绣作品共需要 700 元, 购买 2 件 $A$ 种湘绣作品与 3 件 $B$ 种湘绣作品共需要 1200 元.
(1) 求 $A$ 种湘绣作品和 $B$ 种湘绣作品的单价分别为多少元?
(2) 该国际旅游公司计划购买 $A$ 种湘绣作品和 $B$ 种湘绣作品共 200 件, 总费用不超过 50000 元, 那么最多能购买 $A$ 种湘绣作品多少件?

如图, 在 $\square A B C D$ 中, 对角线 $A C, B D$ 相交于点 $O, \angle A B C=90^{\circ}$.
(1) 求证： $A C=B D$ ；
(2) 点 $E$ 在 $B C$ 边上, 满足 $\angle C E O=\angle C O E$. 若 $A B=6, B C=8$, 求 $C E$ 的长及 $\tan \angle C E O$ 的值.

对于凸四边形，根据它有无外接圆（四个顶点都在同一个圆上）与内切圆（四条边都与同一个圆相切），可分为四种类型，我们不妨约定：
既无外接圆，又无内切圆的四边形称为"平凡型无圆"四边形：
只有外接圆，而无内切圆的四边形称为"外接型单圆"四边形；
只有内切圆，而无外接圆的四边形称为"内切型单圆"四边形：
既有外接圆，又有内切圆的四边形称为"完美型双圆"四边形。
请你根据该约定, 解答下列问题:
（1）请你判断下列说法是否正确（在题后相应的括号中，正确的打" $\sqrt{ }$ "，错误的打" $\times$ "）。
① 平行四边形一定不是"平凡型无圆"四边形；
② 内角不等于 $90^{\circ}$ 的菱形一定是"内切型单圆"四边形；
③ 若"完美型双圆"四边形的外接圆圆心与内切圆圆心重合, 外接圆半径为 $R$, 内切圆半径为 $r$, 则有 $R=\sqrt{2} r$. $\qquad$
(2) 如图1, 已知四边形 $A B C D$ 内接于 $\odot O$, 四条边长满足: $A B+C D \neq B C+A D$.
① 该四边形 $A B C D$ 是" $\qquad$ "四边形（从约定的四种类型中选一种填入）；
② 若 $\angle B A D$ 的平分线 $A E$ 交 $\odot O$ 于点 $E, \angle B C D$ 的平分线 $C F$ 交 $\odot O$ 于点 $F$, 连接 $E F$. 求证: $E F$ 是 $\odot O$ 的直径.

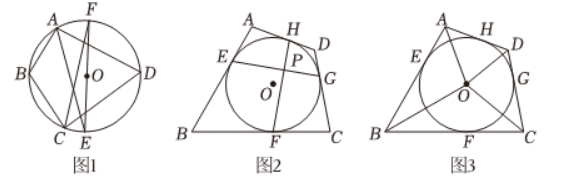
(3) 已知四边形 $A B C D$ 是"完美型双圆"四边形, 它的内切圆 $\odot O$ 与 $A B, B C, C D, A D$ 分别相切于点 $E, F, G, H$.
① 如图2, 连接 $E G, F H$ 交于点 $P$. 求证: $E G \perp F H$ ；
② 如图3, 连接 $O A, O B, O C, O D$, 若 $O A=2, O B=6, O C=3$, 求内切圆 $\odot O$ 的半径 $r$ 及 $O D$ 的长.

已知四个不同的点 $A\left(x_1, y_1\right), B\left(x_2, y_2\right), C\left(x_3, y_3\right), D\left(x_4, y_4\right)$ 都在关于 $x$ 的函数 $y=a x^2+b x+c(a, b, c$是常数, $a \neq 0$ ) 的图象上.
（1）当 $A, B$ 两点的坐标分别为 $(-1,-4),(3,4)$ 时，求代数式 $2024 a+1012 b+\frac{3}{7}$ 的值；
（2）当 $A, B$ 两点的坐标满足 $a^2+2\left(y_1+y_2\right) a+4 y_1 y_2=0$ 时, 请你判断此函数图象与 $x$ 轴的公共点的个数, 并说明理由；
（3）当 $a>0$ 时, 该函数图象与 $x$ 轴交于 $E, F$ 两点, 且 $A, B, C, D$ 四点的坐标满足： $2 a^2+2\left(y_1+y_2\right) a+y_1^2+y_2^2=0,2 a^2-2\left(y_3+\right.$ $\left.y_4\right) a+y_3^2+y_4^2=0$ 。请问是否存在实数 $(m>1)$, 使得 $A B, C D, m \cdot E F$ 这三条线段组成一个三角形, 且该三角形的三个内角的大小之比为 $1: 2: 3$ ? 若存在, 求出 $m$ 的值和此时函数的最小值；若不存在, 请说明理由（注： $m \cdot E F$ 表示一条长度等于 $E F$ 的 $m$ 倍的线段）.