甲同学计划去参观某景点，但门票需在网上预约．该同学从第一天开始，每天在规定的预约时间段开始预约，若预约成功，便停止预约；若连续预约三天都没成功，则放弃预约．假设该同学每天预约门票成功的概率均为 0.7 ，
（1）求甲同学到第三天才预约成功的概率；
（2）记 $X$ 为甲同学预约门票的天数，求 $X$ 的分布列和期望 $E(X)$ ．

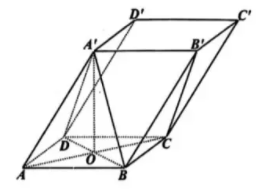
如图，在平行六面体 $A B C D-A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ 中，$A B=A D=2, \angle A^{\prime} A B=\angle A^{\prime} A D$ ，且 $A^{\prime} B \perp A C$ ，设 $A C$ 与 $B D$ 的交于点 $O$ ．
（1）证明：$A^{\prime} O \perp$ 平面 $A B C D$ ；
（2）若 $A A^{\prime}=3$ ，且 $\angle B A D=60^{\circ}$ ，求直线 $A^{\prime} B$ 与平面 $A^{\prime} B^{\prime} C D$ 所成角的正弦值．

已知函数 $f(x)= e ^{a x} \ln x$ ，其中 $a>0$ ．
（1）若 $y=f(x)$ 在点 $(1,0)$ 处的切线与两坐标轴所围成三角形的面积为 $\frac{ e }{2}$ ，求 $a$ 的值；
（2）若 $x=x_0$ 是 $f(x)$ 的极小值点，证明：$f\left(x_0\right) < - e$ ．

已知椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的左顶点为 $A$ ，焦距为 $2 \sqrt{3}$ ，且离心率为 $\frac{\sqrt{3}}{2}$ ．
（1）求椭圆 $C$ 的方程；
（2）直线 $l$ 与椭圆 $C$ 交于 $M, N$ 两点，点 $P$ 为 $\triangle A M N$ 的外心．
（i）若 $\triangle A M N$ 为等边三角形，求点 $P$ 的坐标；
（ii）若点 $P$ 在直线 $x=-\frac{1}{3}$ 上，求点 $A$ 到直线 $l$ 的距离的取值范围．

已知无穷数列 $\left\{a_n\right\}$ 满足 $a_n=q^n(q \neq 0)$ ．对于集合 $T \subseteq N^*$ ，定义 $S_T$ ：若 $T=\varnothing$ ，则 $S_T=0$ ；若 $T=\left\{t_1, t_2, \cdots, t_k\right\}$ ，则 $S_T=a_{t 1}+a_{t_2}+\cdots+a_{t_k}$ ．
（1）若 $q=2, S_T=26$ ，求集合 $T$ ；
（2）若 $q=2$ ，集合 $A, B \subseteq N^*$ ，且 $S_A+S_B=2^{10}$ ，求 $A \cap B$ 中元素个数的可能值：
（3）若 $0 < q < \frac{1}{2}$ ，集合 $A_1, A_2, \cdots, A_n \subseteq N^*$ ，对任意的 $i, j \in N^*, 1 \leq i < j \leq n$ ，满足 $A_i \cap A_j=\varnothing$ ，且 $S_{A_1}>S_{A_2}>\cdots>S_{A_n}>0$ ，证明：$\sum_{k=1}^n \frac{S_{A_k}}{S_{A_1}} < \frac{1-q}{1-2 q}$ ．