单选题 (共 8 题 ),每题只有一个选项正确
命题"$\forall x>0, x+1 \leqslant e ^x$"的否定是
$\text{A.}$ $\exists x \leqslant 0, x+1 \leqslant e ^x$
$\text{B.}$ $\exists x \leqslant 0, x+1> e ^x$
$\text{C.}$ $\exists x>0, x+1 \leqslant e ^x$
$\text{D.}$ $\exists x>0, x+1> e ^x$
已知集合 $A=\left\{x \mid \log _2 x < 2\right\}, B=\{x \mid 1+a < x < 2 a-1\}$ ,若 $A \cap B=\varnothing$ ,则实数 $a$ 的取值范围是
$\text{A.}$ $[3,+\infty)$
$\text{B.}$ $\left(-\infty, \frac{1}{2}\right]$
$\text{C.}$ $(-\infty, 2] \cup[3,+\infty)$
$\text{D.}$ $\left(-\infty, \frac{1}{2}\right] \cup[3,+\infty)$
已知 $\alpha \in\left(0, \frac{\pi}{2}\right)$ ,若 $\sin \left(\frac{3 \pi}{2}+2 \alpha\right)+\cos \left(\alpha-\frac{\pi}{4}\right)=0$ ,则 $\alpha=$
$\text{A.}$ $\frac{\pi}{12}$
$\text{B.}$ $\frac{\pi}{6}$
$\text{C.}$ $\frac{5 \pi}{12}$
$\text{D.}$ $\frac{\pi}{3}$
已知圆台的上,下底面半径分别为 2,4 ,母线与底面所成角为 $\frac{\pi}{4}$ ,则该圆台的体积为
$\text{A.}$ $56 \pi$
$\text{B.}$ $\frac{56 \pi}{3}$
$\text{C.}$ $28 \pi$
$\text{D.}$ $\frac{28 \pi}{3}$
某学习小组共 5 名同学,某次模拟考试的数学成绩平均分数为 112 ,已知其中 4 名同学的成绩分别为 $96,109,120,126$ ,则这 5 名同学成绩的第 75 百分位数是
$\text{A.}$ 112
$\text{B.}$ 119
$\text{C.}$ 120
$\text{D.}$ 121
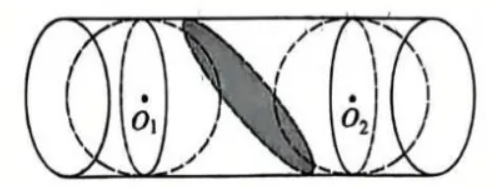
如图,在简高为 16 的圆柱型简中,放置两个半径均为 3 的小球,两个小球均与简壁相切,且分别与两底面相切,已知平面 $\alpha$ 与两个小球也相切,平面 $\alpha$ 被圆筒所栽得到的截面为椭圆,则该椭圆的离心率为
$\text{A.}$ $\frac{1}{3}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $\frac{3}{4}$
$\text{D.}$ $\frac{4}{5}$
在平面直角坐标系 $x O y$ 中,向量 $\overrightarrow{O A}= a =\left(x_1, y_1\right), \overrightarrow{O B}= b =\left(x_2, y_2\right)$ ,若 $a , b$ 不共线,记以 $O A$ , $O B$ 为邻边的平行四边形的面积 $S( a , b )=\left|x_1 y_2-x_2 y_1\right|$ .已知 $\overrightarrow{O M}=m, \overrightarrow{O N}=n, \overrightarrow{O P}= p =\lambda m+$ $\mu n\left(\lambda, \mu \in R , \lambda^2+\mu^2 \neq 0\right)$ ,则 $\frac{S( m , p )+ S( n , p )}{S( m , n )}=$
$\text{A.}$ $|\lambda+\mu|$
$\text{B.}$ $|\lambda \mu|$
$\text{C.}$ $|\lambda|+|\mu|$
$\text{D.}$ $\frac{|\lambda \mu|}{|\lambda|+|\mu|}$
在 $\triangle A B C$ 中,内角 $A, B, C$ 的对边分别为 $a, b, c$ ,若 $a^2, b^2, 2 c^2$ 成等差数列,则 $\tan (C-B)$ 的最小值为
$\text{A.}$ $\frac{1}{3}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $-\frac{2}{3}$
$\text{D.}$ $-\frac{\sqrt{3}}{3}$
多选题 (共 3 题 ),每题有多个选项正确
已知 $a, b, c$ 是三条不同的直线,$\alpha, \beta, \gamma$ 是三个不同的平面,则下列命题中不正确的是
$\text{A.}$ 若 $\alpha \perp \beta, \alpha \perp \gamma, \beta \cap \gamma=c$ ,则 $c \perp \alpha$
$\text{B.}$ 若 $\alpha \perp \beta, \alpha \perp \gamma, a \subset \alpha, a \perp \beta, c \subset \gamma$ ,则 $a \perp c$
$\text{C.}$ 若 $a / / \beta / / \gamma, c / / \gamma, a \subset \alpha, b \subset \beta$ ,则 $a / / b / / c$
$\text{D.}$ 若 $a \perp \alpha, b \perp \beta, c \perp \gamma, a / / b / / c$ ,则 $\alpha / / \beta / / \gamma$
已知函数 $f(x)=\frac{1}{2} \cos \left(2 x-\frac{\pi}{3}\right)$ ,则
$\text{A.}$ $f(x)$ 的图像可以由 $y=\frac{1}{2} \sin 2 x$ 的图象向左平移 $\frac{\pi}{12}$ 个单位长度得到
$\text{B.}$ $f(x)$ 的图象关于 $x=-\frac{\pi}{12}$ 对称
$\text{C.}$ $f(x)$ 在 $\left[\frac{5 \pi}{3}, \frac{13 \pi}{6}\right]$ 上单调递增
$\text{D.}$ $\forall x \in\left(\frac{\pi}{2}, \frac{5 \pi}{6}\right], f(x) \in\left[-\frac{1}{2},-\frac{1}{4}\right]$
已知复数 $z_1, z_2$ 在复平面内对应的点分别为 $Z_1, Z_2, O$ 为坐标原点,则
$\text{A.}$ 若 $z=z_1+z_2$ ,则 $\bar{z}=\overline{z_1}+\overline{z_2}$
$\text{B.}$ 若 $z_1, z_2$ 均不为 0 ,则 $\left|z_1 z_2\right|=\left|\overrightarrow{O Z_1} \cdot \overrightarrow{O Z_2}\right|$
$\text{C.}$ 若 $z=\overline{z_2}$ ,则 $\left|z_1 z_2\right|=\left|z_1 z\right|$
$\text{D.}$ 若 $\left|\overrightarrow{O Z_1}+\overrightarrow{O Z_2}\right|=\left|\overrightarrow{O Z_1}-\overrightarrow{O Z_2}\right|$ ,则 $z_1 \cdot z_2=0$
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知数列 $\left(a_n\right)$ 为等差数列.$a_5=9, a_3+a_6+a_9=33$ .
(1)求数列 $\left\{a_n\right\rangle$ 的通项公式.
(2)若 $b_n+a_n= 19$ ,求数列 $|b_n|$ 的前 $n$ 项和 $S_n$ .
已知函数 $f(x)=x e ^{x}$
(1)求函数 $f(x)$ 的极值.
(2)若 $f(x)-\ln x+a x \geqslant 1$ 但成立,求实数 $a$ 的取值范围.
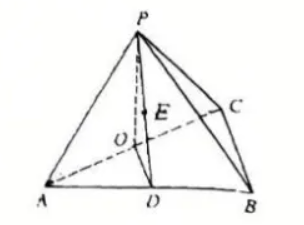
如图.在三棱锥 $P-A B C$ 中.,侧面 $P A C$ 为等腰三角形,$\angle A P C=\frac{2 \pi}{3}, O$ 为 $A C$ 的中点.$D$ 为 $A B$ 的中点.$O P=O D=1 . A B=4$ ,点 $E$ 在 $P D$ 上 .
(1)若 $2 \overrightarrow{P E}=\overrightarrow{P D}$ ,证明,平面 $A C E \perp$ 平面 $P A B$ .
(2)若 $P B=2 \sqrt{2}$ ,求平而 $P A B$ 与平面 $P B C$ 夹角的余弦值
某校开展"强国知识"挑战赛,比赛分为两轮,规则如下:
① 第一轮为"时事政治"试题,共 3 道试题,至少正确回答 2 道,才能进人第二轮,否则挑战失败;第二轮为"科普知识"试题,共 3 道试题,也要至少正确回答 2 道才能算挑战成功,否则挑战失败(进人比赛轮次后,该轮次中所有题目均需要作答);两轮都挑战成功,可以获得"强国小能手"称号;
② 每个参赛组由两人组成,作答方案有两个,第一种方案是在第一轮和第二轮中,两人依次轮流答题(例如:甲先回答第一轮第一题,则乙回答第一轮第二题;甲再回答第一轮第三题;若进人第二轮,则由乙回答第二轮第一题。甲回答第工轮第二题,乙再回答第二轮第三题);第二种方案是由参赛两人分别回答第一轮所有试题和第二轮所有试题(如甲回答第一轮所有试题,则乙回答第二轮的所有试题)。
已知某小组由甲,乙两名同学组成,甲同学正确回答第一轮,第二轮中的每道试题的概率分别为 $\frac{4}{5}, \frac{2}{3}$ ;乙同学正确回答第一轮,第二轮中的每道试题的概率分别为 $\frac{3}{4}, \frac{4}{5}$ .
(1)若该小组采用第一种方案答题,且甲先回答第一轮中的第一题.
(i)求该小组在第一轮中就挑战失败的概率.
(ii)已知该小组获得"强国小能手"称号,求甲正确回答了 3 道试题的概率.
(2)无论采用哪一种作答方案,第一轮第一题均由甲作答,以该小组获得"强国小能手"称号的概率大小为决策依据,应该选择哪一种作答方案?并说明理由.
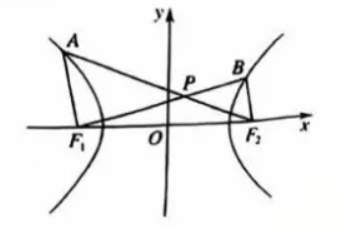
如图,已知 $F_1, F_2$ 为双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的左,右焦点,直线 $y=\frac{\sqrt{2}}{2} x$ 为 $C$ 的一条渐近线,$A, B$ 分别为 $C$ 上位于第二,一象限内的点,$A F_1, B F_2$ 的倾斜角分别为 $\theta_1, \theta_2$ ,且当 $\theta_1=\frac{\pi}{2}$时,$\left|A F_1\right|=\frac{\sqrt{2}}{2}$ .
(1)求双曲线 $C$ 的标准方程.
(2)若 $\theta_1=\theta_2$ ,连接 $A F_2, B F_1$ 相交于 $P$ .
(i)若 $\left|A F_1\right|-2=\left|B F_2\right|$ ,求直线 $B F_2$ 的方程.
(ii)证明:点 $P$ 在以 $F_1, F_2$ 为焦点的椭图上,并求出该椭圆的标准方程.