综合与实践
顺次连接任意一个四边形的中点得到一个新四边形，我们称这个新四边形为原四边形的中点四边形．数学兴趣小组通过作图、测量，猜想：原四边形的对角线对中点四边形的形状有着决定性作用．
以下从对角线的数量关系和位置关系两个方面展开探究．
【探究一】

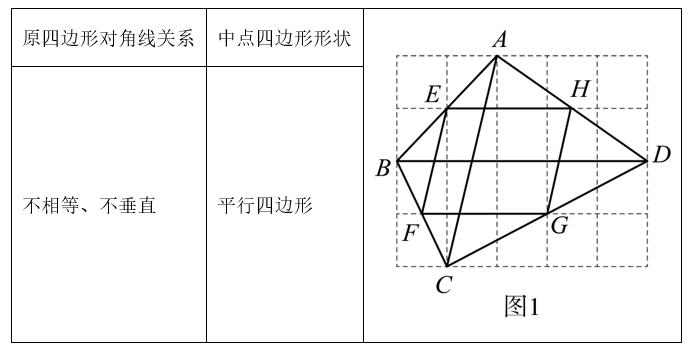
如图 1，在四边形 $A B C D$ 中，$E, ~ F, ~ G, ~ H$ 分别是各边的中点．
求证：中点四边形 $E F G H$ 是平行四边形．
证明：$\because E, ~ F, ~ G, ~ H$ 分别是 $A B, ~ B C, ~ C D, ~ D A$ 的中点，
$\therefore E F, ~ G H$ 分别是 $V A B C$ 和 $V A C D$ 的中位线，
$\therefore E F=\frac{1}{2} A C, \quad G H=\frac{1}{2} A C$ $\qquad$ （1） $\qquad$
$\therefore E F=G H$ ．
同理可得：$E H=F G$ ．
$\therefore$ 中点四边形 $E F G H$ 是平行四边形．
结论：任意四边形的中点四边形是平行四边形．
（1）请你补全上述过程中的证明依据（1） $\qquad$
【探究二】

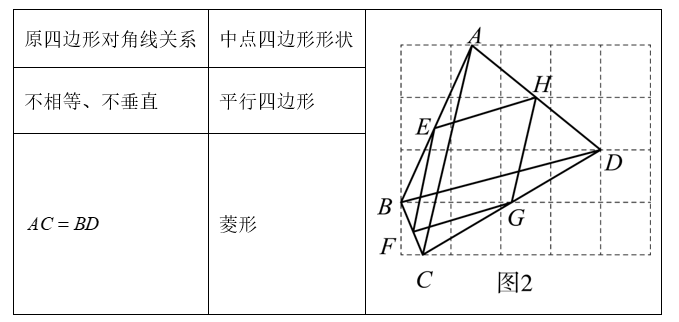
从作图、测量结果得出猜想Ⅰ：原四边形的对角线相等时，中点四边形是菱形．
（2）下面我们结合图2来证明猜想Ⅰ，请你在探究一证明结论的基础上，写出后续的证明过程．
【探究三】

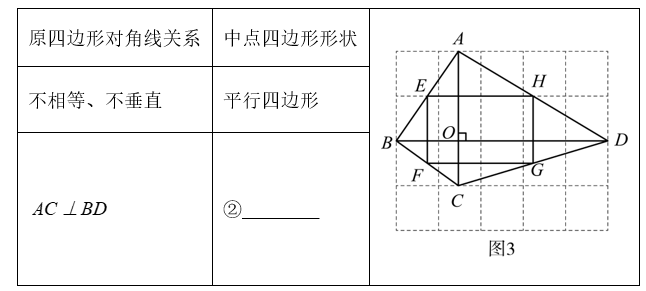
（3）从作图，测量结果得出猜想II：原四边形对角线垂直时，中点四边形是（2） $\qquad$
（4）下面我们结合图 3 来证明猜想II，请你在探究一证明结论的基础上，写出后续的证明过程。
【归纳总结】
（5）请你根据上述探究过程，补全下面的结论，并在图 4 中画出对应的图形．

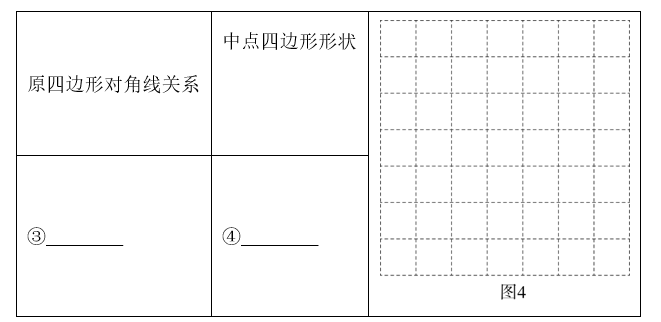
结论：原四边形对角线（3） $\qquad$时，中点四边形是（4） $\qquad$

【问题呈现】
小明在数学兴趣小组活动时遇到一个几何问题：如图（1），在等边 $V A B C$ 中，$A B=3$ ，点 $M, ~ N$ 分别在边 $A C$ ， $B C$ 上，且 $A M=C N$ ，试探究线段 $M N$ 长度的最小值．

【问题分析】
小明通过构造平行四边形，将双动点问题转化为单动点问题，再通过定角发现这个动点的运动路径，进而解决上述几何问题．

【问题解决】
如图（2），过点 $C, ~ M$ 分别作 $M N, ~ B C$ 的平行线，并交于点 $P$ ，作射线 $A P$ ．在【问题呈现】的条件下，完成下列问题：

（1）证明：$A M=M P$ ；
（2）$\angle C A P$ 的大小为＿度，线段 $M N$ 长度的最小值为 $\qquad$ ．
【方法应用】
某种简易房屋在整体运输前需用钢丝绳进行加固处理，如图（3）．小明收集了该房屋的相关数据，并画出了示意图，如图（4）， $V A B C$ 是等腰三角形，四边形 $B C D E$ 是矩形，$A B=A C=C D=2$ 米，$\angle A C B=30^{\circ} . M N$是一条两端点位置和长度均可调节的钢丝绳，点 $M$ 在 $A C$ 上，点 $N$ 在 $D E$ 上．在调整钢丝绳端点位置时，其长度也随之改变，但需始终保持 $A M=D N$ ．钢丝绳 $M N$ 长度的最小值为多少米．

情境 图1是由正方形纸片去掉一个以中心O为顶点的等腰直角三角形后得到的．
该纸片通过裁剪，可拼接为图2所示的钻石型五边形，数据如图所示．
（说明：纸片不折叠，拼接不重叠无缝隙无剩余）

操作 嘉嘉将图1所示的纸片通过裁剪，拼成了钻石型五边形．
如图3，嘉嘉沿虚线 ， 裁剪，将该纸片剪成①，②，③三块，再按照图4所示进行拼接．根据嘉嘉的剪拼过程，解答问题

（1）直接写出线段 的长；
（2）直接写出图3中所有与线段 相等的线段，并计算 的长．
探究淇淇说：将图1所示纸片沿直线裁剪，剪成两块，就可以拼成钻石型五边形．
请你按照淇淇的说法设计一种方案：在图5所示纸片的 边上找一点P（可以借助刻度尺或圆规），画出裁剪线（线段 ）的位置，并直接写出 的长．

如图，在平行四边形 $A B C D$ 中，点 $F$ 在边 $A D$ 上，$A B=A F$ ，连接 $B F$ ，点 $O$ 为 $B F$ 的中点，$A O$ 的延长线交边 $B C$ 于点 $E$ ，连接 $E E$
（1）求证：四边形 $A B E F$ 是菱形：
（2）若平行四边形 $A B C D$ 的周长为 $22, C E=1, \angle B A D=120^{\circ}$ ，求 $A E$ 的长．

如图，在 Rt $\triangle A B C$ 中，$C D$ 是斜边 $A B$ 上的中线，$B E / / D C$ 交 $A C$ 的延长线于点 $E$ ．

（1）请用无刻度的直尺和圆规作 $\angle E C M$ ，使 $\angle E C M=\angle A$ ，且射线 $C M$ 交 $B E$ 于点 $F$（保留作图痕迹，不写作法）．
（2）证明（1）中得到的四边形 $C D B F$ 是菱形

如图，四边形 $A B C D$ 的对角线 $A C$ 与 $B D$ 相交于点 $O, A D / / B C, \angle A B C=90^{\circ}$ ，有下列条件：
① $A B / / C D$ ，（2）$A D=B C$ ．
（1）请从以上 ① ② 中任选 1 个作为条件，求证：四边形 $A B C D$ 是矩形；
（2）在（1）的条件下，若 $A B=3, A C=5$ ，求四边形 $A B C D$ 的面积．

图（1），图（2）均是 $4 \times 4$ 的正方形网格，每个小正方形的顶点称为格点．点 $A, B$ ， $C, D, E, O$ 均在格点上．图（1）中已画出四边形 $A B C D$ ，图（2）中已画出以 $O E$ 为半径的 $e O$ ，只用无刻度的直尺，在给定的网格中按要求画图．

（1）在图（1）中，面出四边形 $A B C D$ 的一条对称轴．
（2）在图（2）中，画出经过点 $E$ 的 $e O$ 的切线．

如图，四边形 $A B C D$ 是矩形，点 $E$ 和点 $F$ 在边 $B C$ 上，且 $B E=C F$ ．求证：$A F=D E$ ．

如图，在四边形 $A B C D$ 中，$\angle A=\angle B=90^{\circ}, O$ 是边 $A B$ 的中点，$\angle A O D=\angle B O C$ ．求证：四边形 $A B C D$ 是矩形。