单选题 (共 4 题 ),每题只有一个选项正确
三角形中最大的内角不能小于( )。
$\text{A.}$ $30^{\circ}$
$\text{B.}$ $45^{\circ}$
$\text{C.}$ $60^{\circ}$
$\text{D.}$ $90^{\circ}$
钝角三角形的高在三角形外的条数是( )。
$\text{A.}$ 0
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ 3
如图 1-4 所示,在 $\triangle A B C$ 中,$A B=6, A C=8$ ,则 $B C$ 边上中线 $A D$ 的取值范围为
$\text{A.}$ $2 < A D < 14$
$\text{B.}$ $1 < A D < 7$
$\text{C.}$ $6 < A D < 8$
$\text{D.}$ $12 < A D < 16$
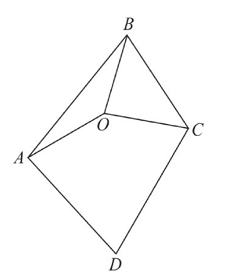
如图 3-1 所示,已知 $O$ 是四边形 $A B C D$ 内一点,$O A=O B=O C$ , $\angle A B C=\angle A D C=70^{\circ}$ ,则 $\angle D A O+\angle D C O$ 的大小是
$\text{A.}$ $70^{\circ}$
$\text{B.}$ $110^{\circ}$
$\text{C.}$ $140^{\circ}$
$\text{D.}$ $150^{\circ}$
填空题 (共 1 题 ),请把答案直接填写在答题纸上
三角形中有一边比第二条边长 3 厘米,这条边又比第三条边短 4 厘米,这个三角形的周长为 28 厘米,求最短边的长.
解答题 (共 11 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
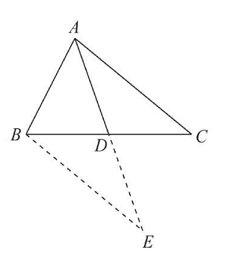
如图 3-2 所示,已知 $A D=B C, A C=B D$ ,求证:$\triangle E A B$ 是等腰三角形.分 析 要判断 $\triangle E A B$ 是等腰三角形,则需得证 $\angle C A B=\angle D B A$ .
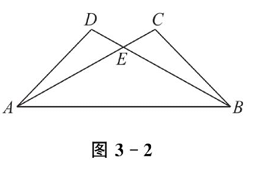
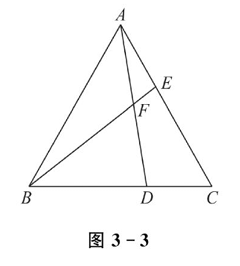
如图 3-3 所示,已知 $\triangle A B C$ 为等边三角形,点 $D, E$ 分别在 $B C$ , $A C$ 边上,且 $A E=C D, A D$ 与 $B E$ 相交于点 $F$ .
(1)求证:$\triangle A B E \cong \triangle C A D$ ;
(2)求 $\angle B F D$ 的度数.
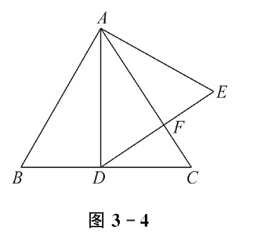
如图 3-4 所示,在边长为 4 的正三角形 $A B C$ 中,$A D \perp B C$ 于点 $D$ ,以 $A D$ 为一边向右作正三角形 $A D E$ 。
(1)求 $\triangle A B C$ 的面积 $S$ ;
(2)判断 $A C, D E$ 的位置关系,并给出证明.
分析 利用等边三角形三线合一的性质。
已知:如图 4-1 所示,Rt $\triangle A B C$ 中,$\angle A C B=90^{\circ}, M$ 是 $A B$ 的中点,$C H \perp A B$ 于 $H, C D$ 平分 $\angle A C B$ .
(1)证明 $\angle D C H=\angle M C D$ .
(2)过点 $M$ 作 $A B$ 的垂线交 $C D$ 延长线于 $E$ ,证明 $C M=E M$ .
(3)猜想 $\triangle A E B$ 是什么三角形?并说明理由.

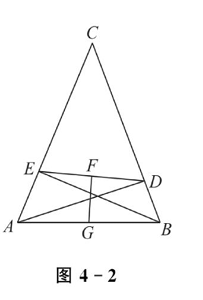
如图 4-2 所示,$A D, B E$ 分别是 $\triangle A B C$ 的边 $B C, A C$ 上的高,$F$ 是 $D E$ 的中点,$G$ 是 $A B$的中点,则 $F G \perp D E$ .
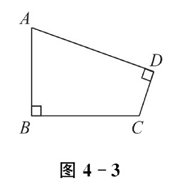
如图 4-3 所示,已知四边形 $A B C D$ 中,$\angle A=60^{\circ}, \angle B=\angle D=90^{\circ}$ , $B C=2, C D=\frac{1}{2}$ ,求 $A B$ .
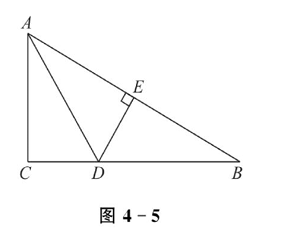
如图 4-5 所示,有一张 Rt $\triangle A B C$ 纸片,$A C=6$ 厘米,$B C=8$ 厘米,现将直角边 $A C$ 沿直线 $A D$ 折叠,使它落在斜边 $A B$ 上,且与 $A E$重合,求 $C D$ 的长.
已知:$a, b, c$ 为 $\triangle A B C$ 三边,且满足 $a^2+b^2+c^2+50=6 a+8 b+10 c$ ,试判断 $\triangle A B C$ 的形状。
如图 5-1 所示,已知:$A B=C D, A C=B D$ ,试证明 $\angle A=\angle D$ .
如图 5-2 所示,在 $\triangle A B E$ 中,$A B=A E, A D=A C, \angle B A D= \angle E A C, B C, D E$ 交于点 $O$ .
求证:
(1)$\triangle A B C \cong \triangle A E D$ ;
(2)$O B=O E$ .

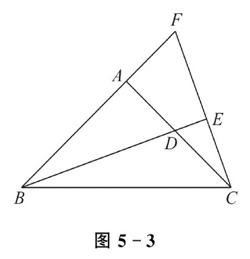
如图 5-3 所示,$\triangle A B C$ 中,$\angle B A C=90^{\circ}, A B=A C, B D$ 是 $\angle A B C$ 的平分线,$B D$ 的延长线垂直于过点 $C$ 的直线于 $E$ ,直线 $C E$交 $B A$ 的延长线于 $F$ .求证:$B D=2 C E$ .
分 析 由已知条件,根据等腰三角形三线合一这一性质,$C E=F E$ ,再证明 $\triangle A B D \cong \triangle A C F$ ,证得 $B D=C F$ ,从而证得 $B D=2 C E$ .
证明题 (共 3 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
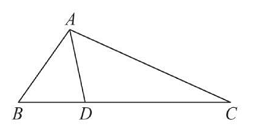
如图 所示,$A D$ 平分 $\angle B A C, A C=A B+B D$ ,求证:$\angle B= 2 \angle C$
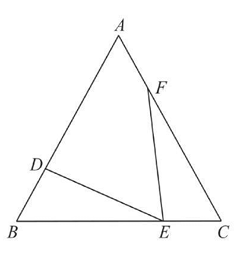
如图 所示,$\triangle A B C$ 是等边三角形,在三边上分别取点 $D$ , $E, F$ ,满足 $A D=B E=F C$ 。
(1)试说明 $D E=E F$ ;
(2)求 $\angle D E F$ 的度数.
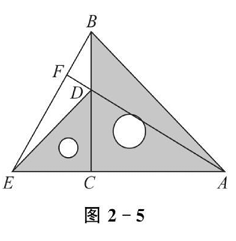
把两个含有 $45^{\circ}$ 角的直角三角板(即 $\triangle A B C$ 与 $\triangle C D E$ 均为等腰直角三角形)按如图2-5所示放置(其中一组直角边重合),先连接 $B E$ ,再连接 $A D$ 并延长交 $B E$ 于点 $F$ .试说明 $A F$ 与 $B E$ 的关系.