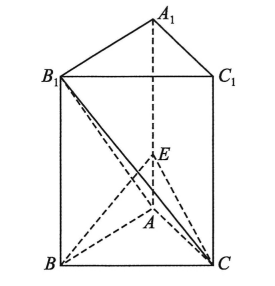
如图，在直三棱柱 $A B C-A_1 B_1 C_1$ 中，$A B=A C=2, A A_1=4, A B \perp A C, A A_1$ 上的点 $E$ 满足 $B E \perp A B_1$ ．
（1）求证：$B E \perp$ 平面 $A B_1 C$ ；
（2）求平面 $C B E$ 与平面 $A B E$ 夹角的余弦值．

已知函数 $f(x)= e ^x-\frac{\ln x}{x}+\frac{a}{x}-1$ ．
（1）若在 $(1, f(1))$ 处的切线斜率为 -1 ，求 $a$ ；
（2）若 $f(x) \geqslant 0$ 恒成立，求 $a$ 的取值范围．

13 张大小质地完全相同的卡牌中有八张数字牌，正面标有 $1 \sim 8$ ，此外还有五张字母牌，正面标有 $A \sim E$ ，将这十三张牌随机排成一行。
（1）求五张字母牌互不相邻的概率；
（2）求在标有 8 的卡牌左侧没有数字牌的概率；
（3）对于给定的整数 $k(1 \leqslant k \leqslant 8)$ ，记＂在标有 $k$ 的数字牌左侧，没有标号比 $k$ 小的数字牌＂为事件 $A_k$ ，求 $A_k$ 发生的概率．（结果用含 $k$ 的式子表示）

已知集合 $A=\{x \mid x=m+\sqrt{3} n, m \in Z , n \in Z \}$ ，集合 $B$ 满足 $B=\left\{x \mid x \in A\right.$ 且 $\left.\frac{1}{x} \in A\right\}$ ．
（1）判断 $2+\sqrt{3}, 3-\sqrt{3}, 0,7+4 \sqrt{3}$ 中的哪些元素属于 $B$ ；
（2）证明：若 $x \in B, y \in B$ ，则 $x y \in B$ ；
（3）证明：若 $x=m+\sqrt{3} n \in B$ ，则 $m^2-3 n^2=1$ ．

如图，椭圆 $\Gamma_1: \frac{x^2}{m}+\frac{y^2}{n}=1(m>n>0), \Gamma_2: \frac{x^2}{n}+\frac{y^2}{m}=1$ ，已知 $\Gamma_1$ 右顶点为 $H(2,0)$ ，且它们的交点分别为 $P_1(1,1), P_2(-1,1), P_3(-1,-1), P_4(1,-1)$ ．
（1）求 $\Gamma_1$ 与 $\Gamma_2$ 的标准方程；
（2）过点 $P_1$ 作直线 $M N$ ，交 $\Gamma_1$ 于点 $M$ ，交 $\Gamma_2$ 于点 $N$ ，设直线 $P_3 M$ 的斜率为 $k_1$ ，直线 $P_3 N$ 的斜率为 $k_2$ ，求 $\frac{k_2}{k_1}$ ；（上述各点均不重合）
（3）点 $Q_1$ 是 $\Gamma_1$ 上的动点，直线 $Q_1 P_1$ 交 $\Gamma_2$ 于点 $Q_2$ ，直线 $Q_2 P_2$ 交 $\Gamma_1$ 于点 $Q_3$ ，直线 $Q_3 P_3$ 交 $\Gamma_2$ 于点 $Q_4$ ，直线 $Q_4 P_4$ 与直线 $Q_1 P_1$ 交于点 $N$ ，求点 $G$ 坐标，使直线 $N G$ 与直线 $N H$的斜率之积为定值．（上述各点均不重合）