单选题 (共 3 题 ),每题只有一个选项正确
设二维连续型随机变量 $(X, Y)$ 的概率密度为
$$
f(x, y)=\left\{\begin{array}{cc}
A\left(x^2+y^2\right), & 0 < x < 2,1 < y < 4, \\
0, & \text { 其他 }
\end{array}\right.
$$
则 $A$ 的值为( ).
$\text{A.}$ $\frac{1}{80}$
$\text{B.}$ $\frac{1}{60}$
$\text{C.}$ $\frac{1}{50}$
$\text{D.}$ $\frac{1}{40}$
设二维连续型随机变量 $(X, Y)$ 的联合概率密度为
$$
f(x, y)=\left\{\begin{array}{lc}
c x^2 y, & x^2 < y < 1, \\
0, & \text { 其他. }
\end{array}\right.
$$
则 $P\{Y \leq X\}=()$ .
$\text{A.}$ $\frac{1}{20}$
$\text{B.}$ $\frac{3}{20}$
$\text{C.}$ $\frac{1}{10}$
$\text{D.}$ $\frac{3}{10}$
设 $X, Y$ 的分布律分别为 $P\{X=0\}=P\{X=1\}=\frac{1}{2}, P\{Y=0\}=\frac{1}{4}, P\{Y=1\}=\frac{3}{4}$ ,且 $P\{X Y=1\}=\frac{1}{2}$ ,则 $P\{X=Y\}=()$ .
$\text{A.}$ $\frac{1}{4}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $\frac{3}{4}$
$\text{D.}$ 1
填空题 (共 5 题 ),请把答案直接填写在答题纸上
设 $(X, Y)$ 的分布函数为 $F(x, y)=a\left(b+\arctan \frac{x}{2}\right)(c+\arctan y)$ ,求常数 $a, b, c$ 的值.
盒子中 5 只球,其中 2 只红球, 3 只白球,从中取球 2 次,每次取 1 只.令
$$
X=\left\{\begin{array}{ll}
0, & \text { 第一次取出红球, } \\
1, & \text { 第一次取出白球. }
\end{array}, Y= \begin{cases}0, & \text { 第二次取出红球, } \\
1, & \text { 第二次取出白球. }\end{cases}\right.
$$
(1)求取出的球不放回时 $(X, Y)$ 的联合分布律;(2)求取出的球放回时 $(X, Y)$ 的联合分布律.
设 $(X, Y)$ 的联合分布函数为
$$
F(x, y)=\left\{\begin{array}{cc}
1-e^{-2 x}-e^{-3 y}+e^{-(2 x+3 y)}, & x \geq 0, y \geq 0, \\
0, & \text { 其他 }
\end{array}\right.
$$
则 $F_X(x)=$ $\qquad$ $F_Y(y)=$ $\qquad$ .
设(X,Y)的联合分布律为
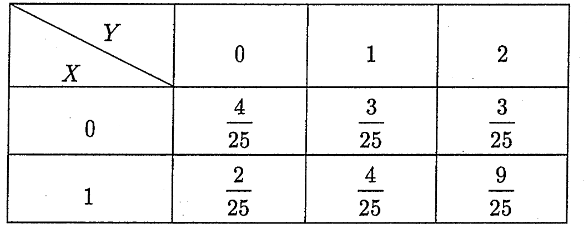
求(X,Y)关于X和关于Y的边缘分布。
随机变量X和Y相互独立,且X的概率分布为
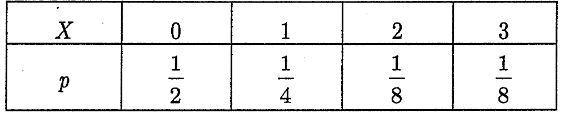
Y的概率分布为

则P{X+Y=2}=().
解答题 (共 8 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设 $(X, Y)$ 在 $x^2+y^2 \leq 5$ 的圆域上服从均匀分布.
(1)求 $(X, Y)$ 的概率密度;
(2)$P\{0 < X < 1,0 < Y < 1\}$ .
设 $(X, Y)$ 在区域 $G=\{(x, y) \mid 0 \leq x \leq 2,0 \leq y \leq 1\}$ 上服从均匀分布,令
$$
U=\left\{\begin{array}{l}
0, X \leq Y, \\
1, X>Y .
\end{array} \quad V=\left\{\begin{array}{l}
0, X \leq 2 Y \\
1, X>2 Y
\end{array}\right.\right.
$$
求 $(U, V)$ 的联合分布律.
设随机变量 $(X, Y)$ 的联合概率密度为
$$
f(x, y)=\left\{\begin{array}{cc}
e^{-x}, & 0 < y < x \\
0, & \text { 其他. }
\end{array}\right.
$$
求边缘概率密度 $f_X(x), f_Y(y)$ .
设平面区域 $G$ 是由 $y=x^2, y=x$ 围成,且二维随机变量 $(X, Y)$ 服从区域 $G$ 上的均匀分布,求 $(X, Y)$ 关于 $X$ 和 $Y$ 的边缘概率密度.
已知(X,Y)的联合分布律为
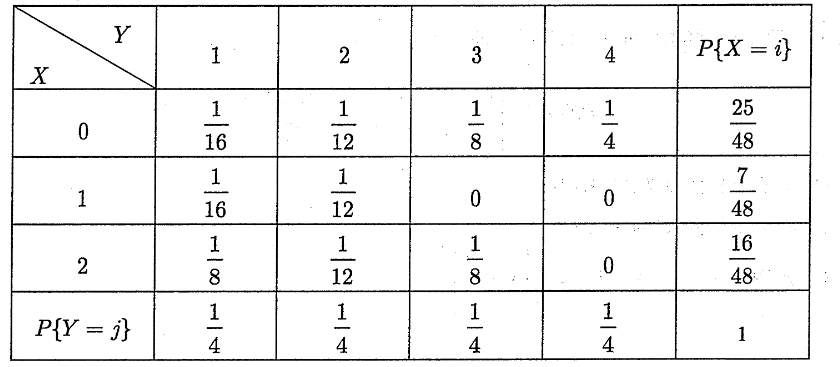
(1)在Y=2的条件下,求X的条件概率分布;
(2)在X=0的条件下,求Y的条件概率分布
设随机变量 $X$ 在区间 $[0,1]$ 上服从均匀分布,当观察到 $X=x(0 < x < 1)$ 时,随机变量 $Y$ 在区间 $(x, 1)$ 上随机地取值,求 $Y$ 的概率密度.
设二维连续型随机变量 $(X, Y)$ 的联合概率密度为
$$
f(x, y)=\left\{\begin{array}{cc}
x^2+\frac{1}{3} x y, & 0 \leq x \leq 1,0 \leq y \leq 2 \\
0, & \text { 其他. }
\end{array}\right.
$$
(1)求 $X$ 和 $Y$ 的边缘概率密度;
(2)求 $X$ 和 $Y$ 的条件概率密度;
(3)求 $P\{X+Y>1\}, P\left\{\left.Y < \frac{1}{2} \right\rvert\, X < \frac{1}{2}\right\}$ .
设二维离散型随机变量(X,Y)的分布律为
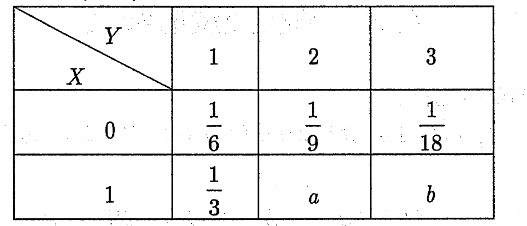
当a,b取何值时,X和Y相互独立?
证明题 (共 4 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设二维随机变量 $(X, Y)$ 的联合概率密度为
$$
f(x, y)=\left\{\begin{array}{lc}
h(x) \cdot g(y), & a \leq x \leq b, c \leq y \leq d \\
0, & \text { 其他. }
\end{array}\right.
$$
其中 $h(x)$ 和 $g(y)$ 非负可积.证明 $X, Y$ 相互独立.
设$(X,Y)$的概率分布为
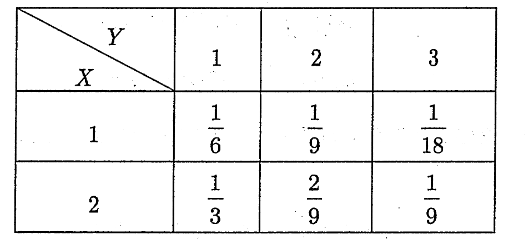
(1)求 $U=\max \{X, Y\}$ 的概率分布;
(2)求 $V=\min \{X, Y\}$ 的概率分布;
(3)求 $Z=X+Y$ 的概率分布.
设二维随机变量 $(X, Y)$ 的概率密度为
$$
f(x, y)=\left\{\begin{array}{cc}
1, & 0 < x < 1,0 < y < 2 x \\
0, & \text { 其他. }
\end{array}\right.
$$
求 $Z=2 X-Y$ 的概率密度 $f_Z(z)$ .
设二维随机变量 $(X, Y)$ 的概率密度为
$$
f(x, y)=\left\{\begin{array}{cc}
2-x-y, & 0 < x < 1,0 < y < 1 ; \\
0, & \text { 其他. }
\end{array}\right.
$$
求 $Z=X+Y$ 的概率密度 $f_Z(z)$ .