单选题 （共 8 题 ），每题只有一个选项正确
函数 $f(x)=\mathrm{e}^x(\sin x+\cos x)$ 在 $x=0$ 处切线的斜率为
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
若 $P$ 为函数 $f(x)=\frac{1}{2} \mathrm{e}^x-\sqrt{3} x$ 图象上的一个动点，以 $P$ 为切点作曲线 $y=f(x)$ 的切线，则切线倾斜角的取值范围是（ ）
$\text{A.}$ $\left[0, \frac{2 \pi}{3}\right)$
$\text{B.}$ $\left(\frac{\pi}{2}, \frac{2 \pi}{3}\right)$
$\text{C.}$ $\left(\frac{2 \pi}{3}, \pi\right)$
$\text{D.}$ $\left[0, \frac{\pi}{2}\right) \cup\left(\frac{2 \pi}{3}, \pi\right)$
曲线 $y=\frac{\mathrm{e}^x}{x+1}$ 在点 $\left(1, \frac{\mathrm{e}}{2}\right)$ 处的切线方程为
$\text{A.}$ $y=\frac{\mathrm{e}}{4} x$
$\text{B.}$ $y=\frac{\mathrm{e}}{2} x$
$\text{C.}$ $y=\frac{\mathrm{e}}{4} x+\frac{\mathrm{e}}{4}$
$\text{D.}$ $y=\frac{\mathrm{e}}{2} x+\frac{3 \mathrm{e}}{4}$
已知直线 $y=x$ 是曲线 $f(x)=\ln x+a$ 的切线，则 $a=$（ ）
$\text{A.}$ -1
$\text{B.}$ 1
$\text{C.}$ -2
$\text{D.}$ 2
如图是函数 $y=f(x)$ 的导函数 $y=f^{\prime}(x)$ 的图象，若 $f(2)=0$ ，则 $y=f(x)$的图象大致为
$\text{A.}$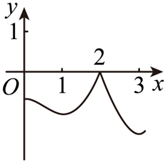 
$\text{B.}$ 
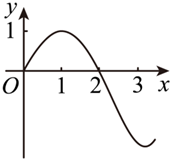$\text{C.}$ 
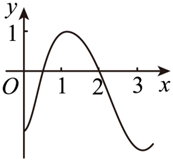$\text{D.}$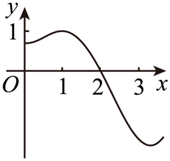 
已知函数 $f(x)=\mathrm{e}^{x-1}+a x^2+1$ 的图象在 $x=1$ 处的切线与直线 $x+3 y-1=0$ 垂直，则实数 $a$ 的值为
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
若经过点 $(a, b)$ 可以且仅可以作曲线 $y=\ln x$ 的一条切线，则下列选项正确的是
$\text{A.}$ $a \leq 0$
$\text{B.}$ $b=\ln a$
$\text{C.}$ $a=\ln b$
$\text{D.}$ $a \leq 0$ 或 $b=\ln a$
已知函数 $f(x)=k \mathrm{e} x-\ln x+1$ 的图象与函数 $g(x)=x \mathrm{e}^{k x}+k x-\mathrm{eln} x$ 的图象有且仅有两个不同的交点，则实数 $k$的取值范围为
$\text{A.}$ $\left(-\frac{1}{\mathrm{e}},-\frac{1}{\mathrm{e}^2}\right) \cup[0,+\infty)$
$\text{B.}$ $\left(-1,-\frac{1}{\mathrm{e}^2}\right) \cup[0, \mathrm{e})$
$\text{C.}$ $\left(-\frac{1}{\mathrm{e}},-\frac{1}{\mathrm{e}^2}\right) \cup[0, \mathrm{e})$
$\text{D.}$ $\left(-1,-\frac{1}{\mathrm{e}^2}\right) \cup[0,+\infty)$
多选题 （共 1 题 ），每题有多个选项正确
已知函数 $f(x)=\mathrm{e}^x+2$（e 为自然对数的底数），则下列结论正确的是
$\text{A.}$ 曲线 $y=f(x)$ 的切线斜率可以是 -2
$\text{B.}$ 曲线 $y=f(x)$ 的切线斜率可以是 3
$\text{C.}$ 过点 $(0,2)$ 且与曲线 $y=f(x)$ 相切的直线有且只有 1 条
$\text{D.}$ 过点 $(1,4)$ 且与曲线 $y=f(x)$ 相切的直线有且只有 2 条
填空题 （共 6 题 ），请把答案直接填写在答题纸上
曲线 $\mathrm{y}=\frac{2 \mathrm{x}-1}{\mathrm{x}+2}$ 在点 $(-1,-3)$ 处的切线方程为
曲线 $y=\ln |x|$ 过坐标原点的两条切线的方程为 $\_\_\_\_$ ， $\_\_\_\_$
过点 $\left(-\frac{2}{3}, 0\right)$ 作曲线 $y=x^3$ 的切线，写出一条切线方程
已知函数 $f(x)=a \mathrm{e}^{2 x}$ 与 $g(x)=2 b \sin x+a(0 < x < \pi)$ ，若曲线 $y=f(x)$ 和 $y=g(x)$ 恰有一个公切点，则 $\frac{a}{b}$ 的最小值是 $\_\_\_\_$ ．
若曲线 $C: f(x)=\left(x^2-4 x+5\right) \mathrm{e}^x-2 \mathrm{e}$ 有三条经过点 $A(a, 0)$ 的切线，则 $a$ 的范围为 $\_\_\_\_$ ．
(2023．天津•统考高考真题）已知函数 $f(x)=\left(\frac{1}{x}+\frac{1}{2}\right) \ln (x+1)$ ．
（1）求曲线 $y=f(x)$ 在 $x=2$ 处切线的斜率；
（2）当 $x>0$ 时，证明：$f(x)>1$ ；
（3）证明：$\frac{5}{6} < \ln (n!)-\left(n+\frac{1}{2}\right) \ln (n)+n \leq 1$ ．
解答题 （共 3 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
设函数 $f(x)=x-x^3 \mathrm{e}^{a x+b}$ ，曲线 $y=f(x)$ 在点 $(1, f(1))$ 处的切线方程为 $y=x+1$ ．
（1）求 $a, b$ 的值；
已知函数 $f(x)=x^3-x, g(x)=x^2+a$ ，曲线 $y=f(x)$ 在点 $\left(x_1, f\left(x_1\right)\right)$ 处的切线也是曲线 $y=g(x)$ 的切线．
（1）若 $x_1=-1$ ，求 $a$ ；
已知函数 $f(x)=\left|e^x-1\right|, x_1 < 0, x_2>0$ ，函数 $f(x)$ 的图象在点 $A\left(x_1, f\left(x_1\right)\right)$ 和点 $B\left(x_2, f\left(x_2\right)\right)$ 的两条切线互相垂直，且分别交 $y$ 轴于 $M, N$ 两点，则 $\frac{|A M|}{|B N|}$ 取值范围是 $\_\_\_\_$ ．